By studying the tensor structure of the gluon propagator, we may be able to determine how well the Landau gauge condition is satisfied, and also discover violations of continuum rotational invariance.
The continuum tensor structure (3) follows from the
condition
q![]() A
A![]() = 0. This translates directly to the lattice
provided we use the symmetric definition of the gluon field. If we
use the asymmetric definition, we will instead obtain the condition
= 0. This translates directly to the lattice
provided we use the symmetric definition of the gluon field. If we
use the asymmetric definition, we will instead obtain the condition
![]() (isin
(isin![]() + cos
+ cos![]() - 1)A'
- 1)A'![]() (
(![]() ) = 0.
) = 0.
The tensor structure may be measured directly by taking the ratios of
different components of
D![]()
![]() (q) for the same value of q.
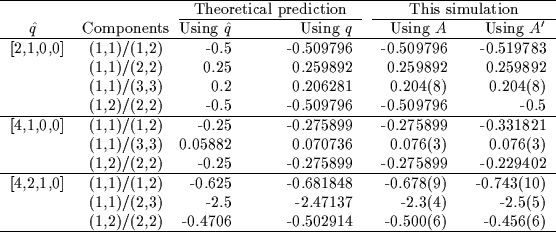
The results for the small lattice are summarised in table
2, and compared to what one would expect from
(3), and to what one would obtain by replacing qwith
(q) for the same value of q.
The results for the small lattice are summarised in table
2, and compared to what one would expect from
(3), and to what one would obtain by replacing qwith ![]() in (3). The results are similar for
the two other lattices.
It is clear from table 2 that our numerical data
are consistent with the expectation from (3). We
can also see that in general, the asymmetric definition A' of the
gluon field gives results which are inconsistent with this form.
in (3). The results are similar for
the two other lattices.
It is clear from table 2 that our numerical data
are consistent with the expectation from (3). We
can also see that in general, the asymmetric definition A' of the
gluon field gives results which are inconsistent with this form.
 |