


Next: TENSOR STRUCTURE
Up: The structure of the propagator
Previous: INTRODUCTION
LATTICE FORMALISM
We use the `symmetric' definition of the gluon field, given
by
U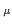 (x) = exp(ig0aA
(x) = exp(ig0aA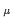 (x +
(x + 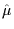 /2)).
This gives the gluon field in momentum space,
/2)).
This gives the gluon field in momentum space,
where 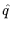 denotes
the discrete momenta
denotes
the discrete momenta
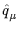 = 2
= 2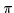 n
n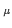 /(aL
/(aL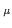 ),
B
),
B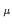 (
(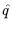 )
)  U
U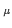 (
(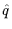 ) - U
) - U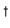
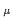 (-
(- 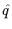 ), and
U
), and
U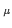 (
(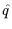 )
) 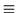
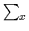 e-i
e-i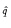 xU
xU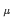 (x). An
alternative, `asymmetric' definition of the gluon field can be
provided by
U
(x). An
alternative, `asymmetric' definition of the gluon field can be
provided by
U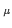 (x) = exp(ig0aA'
(x) = exp(ig0aA'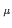 (x)). In momentum space,
this differs from A
(x)). In momentum space,
this differs from A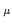 (x) by a factor
exp(i
(x) by a factor
exp(i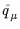 a/2).
a/2).
The gluon propagator
Dab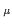
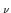 (
(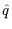 ) is defined as
) is defined as
Dab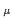 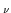 ( (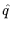 ) = ) = 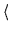 Aa Aa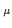 ( (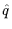 )Ab )Ab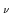 (- (- 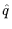 ) ) / V , / V ,
|
(2) |
where
A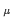 (
( )
) 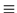 taA
taA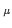 a(
a(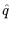 ). In the continuum
Landau gauge, the propagator has the structure
). In the continuum
Landau gauge, the propagator has the structure
D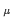 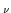 ab(q) = ab(q) = 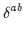 ( (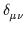 -
- 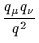 )D(q2) , )D(q2) ,
|
(3) |
At tree level, D(q2) will have the form
D(0)(q2) = 1/q2.
On the lattice, this becomes
D(0)(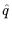 ) = a2/(4
) = a2/(4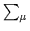 sin2(
sin2(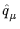 a/2)).
Since QCD is asymptotically free, we expect that up to logarithmic
corrections,
q2D(q2)
a/2)).
Since QCD is asymptotically free, we expect that up to logarithmic
corrections,
q2D(q2)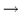 1 in the ultraviolet. Hence we define
the new momentum variable q by
q
1 in the ultraviolet. Hence we define
the new momentum variable q by
q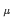
 (2/a)sin(
(2/a)sin(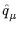 a/2), and use this throughout
a/2), and use this throughout
Table:
Simulation parameters. The lattice spacing is taken from the
string tension [6].
| Name |
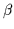 |
a-1 (GeV) |
Volume |
Nconf |
| Small |
6.0 |
1.885 |
163 x 48 |
125 |
| Large |
6.0 |
1.885 |
323 x 64 |
75 |
| Fine |
6.2 |
2.63 |
243 x 48 |
223 |
We have analysed three lattices, with different values for the volume
and lattice spacing. The details are given in
table 1. All the configurations have been fixed to
Landau gauge with an accuracy
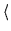 (
(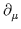 A
A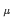 )2
)2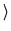 < 10-12.
< 10-12.



Next: TENSOR STRUCTURE
Up: The structure of the propagator
Previous: INTRODUCTION
Jon Ivar Skullerud
1999-02-15
![]() (x) = exp(ig0aA
(x) = exp(ig0aA![]() (x +
(x + ![]() /2)).
This gives the gluon field in momentum space,
/2)).
This gives the gluon field in momentum space,
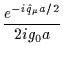
![]()
![]() (
(![]() ) is defined as
) is defined as
![]() (
(![]() A
A![]() )2
)2![]() < 10-12.
< 10-12.