Dr(q2) = 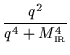 L(q2, MIR) L(q2, MIR)
|
(5) |
We have demonstrated scaling in our lattice data over the entire range of q2 considered, and will now proceed with model fits. The following functional forms have been considered:
Gribov[3]
Stingl[4] Marenzoni[5] Cornwall[6] Model A Model B Model C where D(q2)
M(q2) = M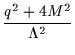 /ln /ln
|
We have also considered the models A and B, which are constructed from models A and B by setting MUV = MIR. Gribov's and Stingl's models (5) and (6) are modified in order to exhibit the asymptotic behaviour of (2). Models A and B are constructed as generalisations of (7) with the correct dimension and asymptotic behaviour.
All models are fitted to the large lattice data using the cylindrical
cut defined in [1,7]. The lowest momentum value was
excluded, as the volume dependence of this point could not be
assessed. In order to balance the sensitivity of the fit between the
high- and low-momentum region, nearby data points within
![]() (qa) < 0.05 were averaged.
(qa) < 0.05 were averaged.
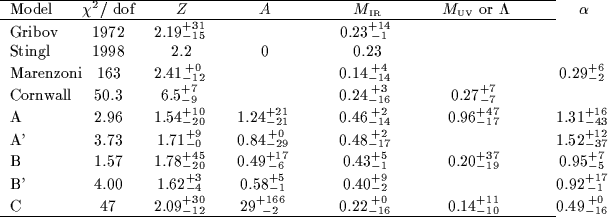
The ![]() per degree of freedom and parameter values for fits to all
these models are shown in table 1. It is clear
that model B accounts for the data better than any of the
other models. The best fit to this model is illustrated in
fig. 2.
per degree of freedom and parameter values for fits to all
these models are shown in table 1. It is clear
that model B accounts for the data better than any of the
other models. The best fit to this model is illustrated in
fig. 2.
 |
![\begin{figure}
\begin{center}
\leavevmode
\mbox{\rotate[l]{\psfig{figure=fit_modelB.ps,height=2.5in} }}
\end{center}\end{figure}](img72.gif) |