


Next: MODEL FITS
Up: Modelling the gluon propagator
Previous: Modelling the gluon propagator
In this note we focus on modelling the gluon propagator calculated in
[1]. We use the same conventions and definitions here as in
[1].
The lattice gluon propagator is related to the renormalised
continuum propagator
DR(q;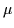 ) via a renormalisation constant,
) via a renormalisation constant,
DL(qa) = Z3(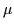 , a)DR(q; , a)DR(q;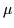 ) . ) .
|
(1) |
The asymptotic behaviour of the renormalised gluon propagator in the
continuum is given to one-loop level by
with dD = 13/44 in Landau gauge for quenched QCD.
Since the renormalised propagator
DR(q;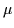 ) is independent of the
lattice spacing, we can use (1) to derive a simple,
q-independent expression for the ratio of the unrenormalised
lattice gluon propagators at the same value of q:
) is independent of the
lattice spacing, we can use (1) to derive a simple,
q-independent expression for the ratio of the unrenormalised
lattice gluon propagators at the same value of q:
where the subscript f denotes the finer lattice (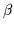 = 6.2 in this
study) and the subscript c denotes the coarser lattice
(
= 6.2 in this
study) and the subscript c denotes the coarser lattice
(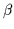 = 6.0). We can use this relation to study directly the scaling
properties of the lattice gluon propagator by matching the data for
the two values of
= 6.0). We can use this relation to study directly the scaling
properties of the lattice gluon propagator by matching the data for
the two values of 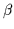 . This matching can be performed by
adjusting the values for the ratios
RZ = Zf/Zc and
Ra = af/ac until the two sets of data lie on the same curve.
We have implemented this by making a linear interpolation of the
logarithm of the data plotted against the logarithm of the momentum
for both data sets. In this way the scaling of the momentum is
accounted for by shifting the fine lattice data to the right by an
amount
. This matching can be performed by
adjusting the values for the ratios
RZ = Zf/Zc and
Ra = af/ac until the two sets of data lie on the same curve.
We have implemented this by making a linear interpolation of the
logarithm of the data plotted against the logarithm of the momentum
for both data sets. In this way the scaling of the momentum is
accounted for by shifting the fine lattice data to the right by an
amount 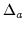 as follows
as follows
lnDc(ln(qac)) = lnDf(ln(qac) - 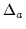 ) + ) + 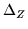
|
(4) |
Here 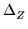 is the amount by which the fine lattice data must be
shifted up to provide the optimal overlap between the two data sets.
The matching of the two data sets has been performed for values of
is the amount by which the fine lattice data must be
shifted up to provide the optimal overlap between the two data sets.
The matching of the two data sets has been performed for values of
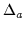 separated by a step size of 0.001.
separated by a step size of 0.001. 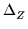 is
determined for each value of
is
determined for each value of 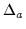 considered, and the optimal
combination of shifts is identified by searching for the global
minimum of the
considered, and the optimal
combination of shifts is identified by searching for the global
minimum of the 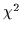 /dof. The ratios Ra and RZ are related
to
/dof. The ratios Ra and RZ are related
to 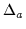 and
and 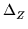 by
Ra = exp(-
by
Ra = exp(- 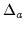 );
RZ = Ra2exp(-
);
RZ = Ra2exp(- 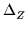 ).
).
We considered matching the lattice data
using
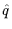 = 2
= 2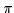 n/L as the momentum variable. The minimum value for
n/L as the momentum variable. The minimum value for
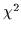 /dof of about 1.7 was obtained for
Ra
/dof of about 1.7 was obtained for
Ra 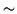 0.815. This value
for Ra is considerably higher than the value of
0.716
0.815. This value
for Ra is considerably higher than the value of
0.716 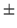 0.040obtained from an analysis of the static quark potential in [2].
From this discrepancy, as well as the relatively high value for
0.040obtained from an analysis of the static quark potential in [2].
From this discrepancy, as well as the relatively high value for
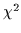 /dof, we may conclude that the gluon propagator, taken as a
function of
/dof, we may conclude that the gluon propagator, taken as a
function of 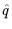 , does not exhibit scaling behaviour for the values
of
, does not exhibit scaling behaviour for the values
of 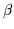 considered here.
considered here.
Fig. 1 shows the result of
the matching using
q = 2sin(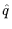 /2) as the momentum
variable. This gives much more
satisfactory values both for
/2) as the momentum
variable. This gives much more
satisfactory values both for 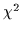 /dof and for Ra. The minimum
value for
/dof and for Ra. The minimum
value for 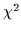 /dof of 0.6 is obtained for Ra = 0.745. Taking a
confidence interval where
/dof of 0.6 is obtained for Ra = 0.745. Taking a
confidence interval where
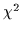 /dof <
/dof < 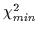 + 1 gives
us an estimate of
Ra = 0.745$
+ 1 gives
us an estimate of
Ra = 0.745$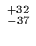 $, which is fully compatible
with the value [2] of
0.716
$, which is fully compatible
with the value [2] of
0.716 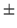 0.040.
0.040.
Figure:
 per degree of freedom as a function of the ratio of
lattice spacings for matching the small and fine lattice data, using
q as the momentum variable. The dashed line indicates the
ratio RZ of the renormalisation constants.
per degree of freedom as a function of the ratio of
lattice spacings for matching the small and fine lattice data, using
q as the momentum variable. The dashed line indicates the
ratio RZ of the renormalisation constants.
![\begin{figure}
\begin{center}
\leavevmode
\rotate[l]{\psfig{figure=MatchBetaLattmom.ps,height=2.2in} }
\end{center}\end{figure}](img50.gif) |



Next: MODEL FITS
Up: Modelling the gluon propagator
Previous: Modelling the gluon propagator
Jon Ivar Skullerud
1999-02-15
![]() ) via a renormalisation constant,
) via a renormalisation constant,
![]() ) is independent of the
lattice spacing, we can use (1) to derive a simple,
q-independent expression for the ratio of the unrenormalised
lattice gluon propagators at the same value of q:
) is independent of the
lattice spacing, we can use (1) to derive a simple,
q-independent expression for the ratio of the unrenormalised
lattice gluon propagators at the same value of q:
![]() = 2
= 2![]() n/L as the momentum variable. The minimum value for
n/L as the momentum variable. The minimum value for
![]() /dof of about 1.7 was obtained for
Ra
/dof of about 1.7 was obtained for
Ra ![]() 0.815. This value
for Ra is considerably higher than the value of
0.716
0.815. This value
for Ra is considerably higher than the value of
0.716 ![]() 0.040obtained from an analysis of the static quark potential in [2].
From this discrepancy, as well as the relatively high value for
0.040obtained from an analysis of the static quark potential in [2].
From this discrepancy, as well as the relatively high value for
![]() /dof, we may conclude that the gluon propagator, taken as a
function of
/dof, we may conclude that the gluon propagator, taken as a
function of ![]() , does not exhibit scaling behaviour for the values
of
, does not exhibit scaling behaviour for the values
of ![]() considered here.
considered here.
![]() /2) as the momentum
variable. This gives much more
satisfactory values both for
/2) as the momentum
variable. This gives much more
satisfactory values both for ![]() /dof and for Ra. The minimum
value for
/dof and for Ra. The minimum
value for ![]() /dof of 0.6 is obtained for Ra = 0.745. Taking a
confidence interval where
/dof of 0.6 is obtained for Ra = 0.745. Taking a
confidence interval where
![]() /dof <
/dof < ![]() + 1 gives
us an estimate of
Ra = 0.745$
+ 1 gives
us an estimate of
Ra = 0.745$![]() $, which is fully compatible
with the value [2] of
0.716
$, which is fully compatible
with the value [2] of
0.716 ![]() 0.040.
0.040.
![\begin{figure}
\begin{center}
\leavevmode
\rotate[l]{\psfig{figure=MatchBetaLattmom.ps,height=2.2in} }
\end{center}\end{figure}](img50.gif)