Kvantefeltteoriens fysiske grunnbegreper

Kvantefeltteorien er en relativistisk, kvantemekanisk mangepartikkelteori. Den tar utgangspunkt i de kvantemekaniske grunnbegrepene operator og tilstand og de feltteoretiske begrepene felt og Lagrangetetthet, og er dessuten karakterisert ved en omfattende vekt på symmetrier og invarianser som er felles for kvantemekanikk og feltteori. Med utgangspunkt i dette begrepsapparatet behandler den systemer av elementære eksitasjoner (`forstyrrelser' i energitetthet, ladningstetthet, impulstetthet osv.), og beskriver hvordan disse eksitasjonene oppstår og forsvinner eller på andre måter forholder seg til hverandre. Dersom en identifiserer de elementære eksitasjonene med elementærpartikler, blir kvantefeltteorien teorien for elementærpartiklene og deres vekselvirkning. Det er som dette jeg skal behandle den her.³⁹

Felt og Lagrangetetthet. Symmetrier i klassisk fysikk

Et felt er i klassisk teori definert som en størrelse som har en bestemt verdi (eller flere, for vektor- og tensorfelt) for hvert punkt i rommet og til hvert tidspunkt. Matematisk kan det altså defineres som en funksjon av koordinatene i det 4-dimensjonale tid-rommet: $\Phi$ = $\Phi$(x) = $\Phi$($\vec{r}\,$, t). Kvantemekanisk må dette, som vi skal se, modifiseres på grunn av det kvantemekaniske ubestembarhetsprinsippet -- men det grunnleggende står igjen, nemlig at feltet forefinnes overalt; det er på et vis definert overalt i tid-rommet, og er altså ikke lokalisert til ett område. Hvert felt representerer i klassisk teori ett bestemt fysisk fenomen -- f.eks. elektrisitet, magnetisme, gravitasjon, lyd. I kvantefeltteorien er det karakteristisk at hvert felt representerer en bestemt partikkeltype. På vilken måte det skjer, håper jeg etterhvert blir klart.

En konstruerer en Lagrangetetthet $\cal$L = $\cal$L($\Phi$,$\partial$$\Phi$/$\partial$x_$\mu$) som en funksjon av feltet og dets deriverte; denne er liksom feltet definert overalt. Når Lagrangetettheten er gitt, er alle feltets dynamiske egenskaper gitt, og i klassisk teori følgelig også feltets fullstendige oppførsel (når randverdiene for feltet er kjent). Dette fremkommer ved at en krever at virkningen, som er integralet av Lagrangetettheten over hele det 4-dimensjonale tid-rommet, skal ha et minimum (eller en stasjonær verdi) for de faktisk forekommende feltverdier -- altså: Man velger de verdier for feltet og dets deriverte som gjør virkningen minst mulig (eller rettere sagt: stasjonær mhp. variasjoner i feltverdiene). I matematisk språk: $\delta$S = $\delta$$\int$$\cal$Ld⁴x = 0. Dette prinsippet, som først ble formulert av Hamilton, kan formuleres fullstendig uavhengig av vilket koordinatsystem man måtte finne på å operere i, og utgjør kanskje den mest mulig invariante (generelle) formen et fysisk prinsipp kan ha. Teorien er lokal, dvs. at feltenes oppførsel et sted bare bestemmes av verdiene på feltet like i nærheten. Dette sikres av at $\cal$L(x) bare avhenger av verdiene for feltene og deres deriverte i punktet x.

Dersom det fysiske systemet man studerer har en bestemt symmetri, dvs. at systemets oppførsel er `symmetrisk' må også Lagrangetettheten som beskriver systemet ha den samme symmetrien. Dersom f.eks. systemets oppførsel er den samme om vi roterer systemet, må også Lagrangetettheten være uforandret ved en slik rotasjon. Denne symmetrien kan også beskrives ved at virkningen forblir den samme ved bestemte typer forandringer i koordinater og felt. Det kan vises at det til enhver slik symmetri i systemet svarer en størrelse som er bevart -- som ikke forandres over tid. Man kan dermed finne ut ganske mye om systemet ved å studere de symmetriene det skal ha. Dersom man i tillegg har en symmetrisk begynnelsestilstand, vet man at systemet alltid vil være i en symmetrisk tilstand.

Symmetriprinsippene kan sies å ha en noe annen status enn de `vanlige' naturlovene. De avgjør til en viss grad vilken form naturlovene kan eller må ha -- altså hva slags naturlover som er mulige eller hva som må kreves av en naturlov. Man kan blant annet knytte symmetriene til begrepet om et gjentagbart eksperiment -- nærmere bestemt til muligheten for å kunne gjenta et eksperiment under ulike forhold (f.eks. forskjellige steder eller med apparaturen i forskjellige retninger) og fremdeles si at det er det samme eksperimentet. De kan også knyttes direkte til begrepet om en naturlov -- går det an å si at naturlovene er forskjellige i forskjellige retninger? Selv om man bør være forsiktig med å si at symmetriprinsippene er a priori betingelser for all naturvitenskap -- det har vist seg at åpenbare symmetriprinsipper ikke har holdt stikk -- er i hvert fall en viss symmetri nødvendig. Wigner har diskutert disse spørsmålene grundigere i flere artikler i [28]. Slike spørsmål knytter også opp mot de mer filosofiske spørsmålene om absolutt rom, absolutt tid osv. Kosmologien har et problematisk forhold til symmetriprinsippene, ettersom man der ikke nødvendigvis kan ta det for gitt at alle tider, steder og retninger er likeverdige, men til en viss grad vil prøve å forklare hvorfor det er slik.

De viktigste symmetriene og bevaringslovene i klassisk fysikk er:

1. Romtranslasjon.

Det er et opplagt krav (synes vi nå) til en fysisk teori at lovene skal være de samme uansett hvor vi befinner oss. Dersom lovene et annet sted i universet skulle være forskjellige fra våre, må begge sett med lover være spesialtilfelle av en mer generell lov, som gjelder overalt. Dessuten har vi ingen grunn til å tro at universet oppviser uregelmessigheter i rommet som er prinsipielt umulig å flytte eller utjevne. Dette formuleres som at systemet er invariant mhp. en translasjon i rommet, dvs. at ingenting i fysikken forandres om en gir alle romkoordinater et fast tillegg: $\vec{r}\,$ $\rightarrow$ $\vec{r}\,$ + $\vec{a}\,$, der $\vec{a}\,$ er en konstant vektor. Den bevarte størrelsen som svarer til denne symmetrien er impulsen -- til det fundamentale fysiske prinsippet om at alle steder i universet er likeverdige (som fulgte av oppbruddet fra aristotelisk fysikk) svarer den fundamentale loven om impulsbevaring (formulert første gang -- i en feilaktig versjon -- av Descartes).

2. Tidstranslasjon.

En av fysikkens oppgaver er å finne lover som gjelder til alle tider. Dersom man finner ut at de fysiske lovene forandrer seg med tida, tvinges man til å søke etter de lovene som styrer denne forandringen -- og disse lovene må naturligvis være tidsuavhengige. En vilken som helst situasjon må også prinsipielt kunne tenkes å gjenta seg på et vilket som helst senere tidspunkt -- det finnes ikke noe absolutt tidspunkt som vi kan fiksere vår tidskoordinat etter. Big Bang-teorien representerer et problem for dette prinsippet, ettersom man her påstår at hele universet skulle ha oppstått fra en singularitet for 15 milliarder år siden. På dette tidspunktet tenker man seg også at alle fysiske lover, samt begrepene om rom og tid, kan bryte sammen. Samtidig er denne teorien også basert på prinsippet om at lovene ikke forandrer seg. Man kan si at det her er snakk om en randbetingelse som ikke er symmetrisk, mens lovene er det. Når systemet vårt er lik hele universet, kan det imidlertid være vanskelig å skille mellom hva som er lover og hva som er resultat av randbetingelser.

Ser en bort fra akkurat dette problemet (som uansett ikke spiller særlig rolle på `normale' skalaer), kan en fastslå at alle egenskaper ved et system blir uforandret om vi `flytter' systemet en tid t₀ frem eller tilbake, altså forandrer tidskoordinaten slik at t $\rightarrow$ t + t₀. Til dette første fysiske grunnprinsipp (anerkjent så lenge det har eksistert en fysikk) svarer den mest fundamentale fysiske loven: Energibevaringen (først formulert i en ufullstendig versjon av Leibniz). Etter Einsteins påvisning av ekvivalensen mellom masse og energi, er også det urgamle prinsippet om materiens konstans blitt trukket inn i denne loven.

3. Rotasjon.

Et tredje symmetriprinsipp som vi går ut fra i våre fysiske betraktninger, er at universet ser (noenlunde) likt ut i alle retninger, og at fysikkens lover ikke tar hensyn til retninger. Dersom vi dreier vårt koordinatsystem med en fast vinkel rundt en eller annen akse i forhold til det fysiske systemet, skal det altså ikke gjøre noen forskjell. Til denne symmetrien svarer loven om dreieimpulsbevaring, altså at summen av dreieimpulsene $\vec{L}\,$ = $\vec{r}\,$ x $\vec{p}\,$ for alle partikler i systemet er bevart.⁴⁰

I praksis oppfatter en gjerne deler av systemet som gitt -- som noe som ligger fast. Dette kan da definere faste steder og retninger i rommet, og verken impuls eller dreieimpuls er bevart for resten av systemet. F.eks. oppfattes gjerne atomkjernene som gitt når vi studerer elektronenes oppførsel i et toatomig molekyl, og linjen mellom dem definerer en retning i rommet. Dermed har vi ikke full rotasjonssymmetri, men vi har fremdeles symmetri ved rotasjoner rundt denne linjen (aksen). I et system med ett sentrum (som et atom eller et solsystem), eller et system der alle partikler eller deler er likeverdige, derimot, har vi i utgangspunktet full rotasjonssymmetri. Disse opplysningene kan brukes til å finne ut ganske mye om vilken form funksjoner som beskriver systemet må ha -- utover bevaringssatsene. I kvantemekanikken blir dette enda mer fremtredende, både fordi det er flere (abstrakte) symmetrier en kan utnytte, og fordi kvantemekanikkens begreper om operator og tilstand er svært godt egnet til å beskrive symmetritransformasjoner -- vi kan her f.eks. skape symmetriske tilstander fra usymmetriske.

4. Relativistisk invarians.

Relativitetsprinsippet -- at to systemer som er i jevn, rettlinjet bevegelse i forhold til hverandre er likeverdige, at fysikkens lover er de samme i alle slike inertialsystemer, og at det ikke finnes noen måte å avgjøre om et system er i ro -- ble først formulert av Galilei og er innbakt i den Newtonske fysikken. Med den spesielle relativitetsteorien og prinsippet om at lyshastigheten er den samme i alle systemer, blir relativistisk invarians (Lorentzinvarians) et eksplisitt krav som en kan ta hensyn til eller ikke i sine modeller. (I systemer hvor alle hastigheter er små behøver en ikke å ta hensyn til det.) Dette kravet begrenser sterkt hva slags størrelser en kan operere med -- f.eks. har en allerede sagt ganske mye om hva slags felt som er tillatt ved å si at Lagrangetettheten må være Lorentz-skalar.

Relativitetsteorien behandler rom og tid under ett, ut ifra erkjennelsen at man ikke kan innføre et absolutt skille mellom tid og rom, dvs. et skille som gjelder i alle inertialsystemer. En kaller derfor det 4-dimensjonale tid-rommet ofte bare for rommet, som er sammensatt av hendelser eller punkter x = (t,$\vec{r}\,$) = (t, x₁, x₂, x₃). Selv om verdien på de fire koordinatene til et punkt vil være forskjellig i forskjellige systemer, er avstanden eller intervallet

$$\Delta$$x²$$\;\stackrel{\rm def}{=}\;$$c²$$\Delta$$t² - $$\Delta$$$$\vec{r}^{2}_{}$$ = c²(t₂ - t₁)² - ($$\vec{r_2}\,$$ - $$\vec{r_1}\,$$)²

mellom to punkter alltid den samme. For $\Delta$x² = 0 følger dette direkte av prinsippet om at lyshastigheten er en universell konstant. Dersom $\Delta$x² < 0, dvs. $\Delta$$\vec{r}^{2}_{}$ > c²$\Delta$t², sier vi at avstanden mellom de to punktene er rom-lik. Da er de to punktene helt separate -- et signal fra det ene kan ikke nå det andre. Vi kan også snakke om rom-like (tredimensjonale) `flater', som er slik at avstanden mellom alle punktene på `flaten' er rom-lik. En slik flate vil være rom-lik i alle inertialsystemer. Et eksempel på en rom-lik flate er alle punktene i rommet ved et gitt tidspunkt. Dersom $\Delta$x² > 0, er avstanden tid-lik. Lyskjegla til et visst punkt utgjøres av de punktene som har avstand 0 til dette punktet, eller m.a.o. de punktene som kan nås med et lyssignal fra dette punktet. Vi kan da si at avstander `innenfor' lyskjegla er tid-like, mens avstander `utenfor' er rom-like.

En fysisk størrelse A karakterisert ved 4 tall (A₀, A₁, A₂, A₃) = (A₀,$\vec{A}\,$) slik at A²$\;\stackrel{\rm def}{=}\;$A₀² - $\vec{A}^{2}_{}$ er den samme i alle inertialsystemer kalles en 4-vektor. 4-vektorer spiller en overmåte stor rolle i relativitetsteorien, ikke minst fordi en kan bruke dem til å konstruere Lorentz-invariante størrelser. Eksempler på 4-vektorer er posisjon x = (ct,$\vec{r}\,$) og impuls p = (E, c$\vec{p}\,$) til en partikkel. Mange felt, deriblant det elektromagnetiske feltet og alle andre gauge-felt, er karakterisert ved 4-vektorer.

   
Tilstander og operatorer i kvantemekanikken

Kvantemekanikken karakteriseres (og skiller seg fra klassisk fysikk og `sunt vett') først og fremst ved det en kan kalle ubestembarhetsprinsippet. Dette kan formuleres på en rekke forskjellige måter og er nedfelt i en rekke av kvantemekanikkens grunnprinsipper. I korthet går det ut på at en ikke kan tilordne alle fysiske størrelser knyttet til et system bestemte verdier overalt og samtidig. Den mest berømte formuleringen av prinsippet er Heisenbergs uskarphetsrelasjon, som angir en grense for den nøyaktigheten man kan måle to fysiske størrelser med samtidig. Før jeg ser nærmere på denne grunnleggende relasjonen, vil jeg imidlertid gjøre rede for hvordan ubestembarhetsprinsippet nedfelles i kvantemekanikkens tilstandsbegrep.

Tilstanden (tilstandsfunksjonen eller tilstandsvektoren) utgjør den mest mulig fullstendige beskrivelsen av et system.⁴¹ Har man bestemt et systems totaltilstand, har man bestemt alt som er mulig å bestemme ved systemet. Tilstanden betegnes $\Psi$ eller  | $\Psi$$\rangle$. Mengden av alle mulige tilstander for et system kalles tilstandsrommet.

Tilstandene oppfyller superposisjonsprinsippet -- dvs. at summen (eller en linærkombinasjon) av to tilstander også er en tilstand. Her er det ubestembarhetsprinsippet kommer inn: Dersom $\Psi_{1}^{}$ betegner en tilstand hvor en bestemt fysisk størrelse i systemet har verdien a₁, og $\Psi_{2}^{}$ en hvor den har verdien a₂, vil begge verdiene forekomme når systemet er i tilstanden $\Psi_{1}^{}$ + $\Psi_{2}^{}$. Derimot vil det ikke forekomme noen andre verdier for denne størrelsen -- de to verdiene vil ikke bli `blandet'.

Jeg kan illustrere dette med et eksempel, som viser hvordan kvantemekanikken på dette punktet bryter med alminnelig, sunt vett. La oss tenke oss at systemet vårt er en kule som har evnen til å skifte farge, på en slik måte at den alltid er ensfarget. Hver farge den kan ha representerer en tilstand av systemet (altså kula). La $\Psi_{1}^{}$ betegne tilstanden at kula er rød, mens $\Psi_{2}^{}$ betegner at kula er blå. Dersom kula vår er et kvantemekanisk system, er $\Psi_{1}^{}$ + $\Psi_{2}^{}$ en tillatt tilstand. Denne tilstanden vil da ikke betegne at kula er fiolett, men at den er både rød og blå. Den betegner heller ikke at f.eks. halve kula er rød og halve kula er blå -- husk at kula alltid er ensfarget. $\Psi_{1}^{}$ + $\Psi_{2}^{}$ betegner altså en tilstand hvor kula er ensfarget rød og blå over det hele! At vi kan si noe slikt, betinger naturligvis at vi ikke ser etter hva slags farge kula har -- det er vanskelig å forestille seg at vi kan se noe ensfarget rødt og blått. Imidlertid kan vi ikke utelukke at denne tilstanden har noen andre merkelige egenskaper som gjør at vi kan slutte oss til at kula faktisk har vært ensfarget rød og blå mens vi ikke så på den.

I tilfellet ovenfor var det, siden vi visste mye om tilstandene $\Psi_{1}^{}$ og $\Psi_{2}^{}$, naturlig å uttrykke den tredje tilstanden vha disse to. Vi sier at vi dekomponerer $\Psi$ i $\Psi_{1}^{}$ og $\Psi_{2}^{}$ -- $\Psi$ inneholder en komponent av $\Psi_{1}^{}$ og en komponent av $\Psi_{2}^{}$. Dette er helt analogt med hvordan vi dekomponerer (eller adderer) vektorer -- tilstandene kan tenkes som vektorer (men ikke i vårt vanlige rom -- tilstandsrommet har gjerne uendelig mange `dimensjoner'). For å fortsette i analogien, kan en si at det er bare `retningen' på tilstanden som spiller noen rolle -- dersom vi multipliserer tilstanden med et vilkårlig (komplekst) tall, blir ingen fysiske egenskaper forandret.

Fra $\Psi_{1}^{}$ og $\Psi_{2}^{}$ kan vi konstruere alle mulige tilstander av kula med ulike `mengder' av rødt og blått -- alle tilstander som inneholder bare rødt og blått, er avhengige av (kan uttrykkes ved eller dekomponeres i) $\Psi_{1}^{}$ og $\Psi_{2}^{}$. Vi kan imidlertid aldri få noen tilstander hvor noe gult forekommer -- alle tilstander av kula som inneholder noe gult er uavhengige av $\Psi_{1}^{}$ og $\Psi_{2}^{}$. Har vi imidlertid en tilstand $\Psi_{3}^{}$ som inneholder noe gult, samt muligens noe rødt og blått, kan alle tilstander med bare rødt, gult og blått i seg dekomponeres i $\Psi_{1}^{}$, $\Psi_{2}^{}$ og $\Psi_{3}^{}$. $\Psi_{3}^{}$ kan da sies å definere en tredje `dimensjon' i tilstandsrommet i forhold til $\Psi_{1}^{}$ og $\Psi_{2}^{}$.

I stedet for å dekomponere alle røde og blå tilstander i $\Psi_{1}^{}$ og $\Psi_{2}^{}$, kunne vi dekomponert dem i f.eks. $\Psi_{1}^{}$ og $\Psi_{2}{^\prime}$ = ${\frac{1}{2}}$$\Psi_{1}^{}$ + $\Psi_{2}^{}$(dersom vi av en eller annen grunn visste mye om denne tilstanden). Vår $\Psi$ ville da bli skrevet $\Psi$ = ${\frac{1}{2}}$$\Psi_{1}^{}$ + $\Psi_{2}{^\prime}$, og det ser ut som om den inneholder mindre av den rene røde tilstanden $\Psi_{1}^{}$ enn i det forrige bildet. Dette ser ut til å gi en flertydighet i beskrivelsen. En kan imidlertid få et entydig uttrykk for hvor mye to tilstander $\Psi$ og $\Phi$ inneholder av hverandre ved å se på produktet (skalarproduktet) $\langle$$\Phi$ | $\Psi$$\rangle$, som er et (komplekst) tall. Dersom produktet av to tilstander er null, sies de å stå normalt på hverandre, og inneholder altså ingenting av hverandre. (Dette er helt analogt med skalarproduktet i vektorregningen.) Produktet av en tilstand med seg selv gir `lengden' av tilstanden; de fysiske tilstandene har alle samme lengde (som regel 1).

Et sett av tilstander  | n$\rangle$ som står normalt på hverandre, har lengde 1 og som er slik at alle mulige tilstander kan dekomponeres i tilstander fra dette settet:

| $$\Psi$$$$\rangle$$ = $$\sum_{n}^{}$$$$\alpha_{n}^{}$$ | n$$\rangle$$ hvor  $$\langle$$m | n$$\rangle$$ = $$\delta_{mn}^{}$$ = $$\left\{\vphantom{ \begin{array}{ll} 1 &; m=n\\ 0 &; m\neq n \end{array} }\right.$$$$\begin{array}{ll} 1 &; m=n\\ 0 &; m\neq n \end{array}$$ $$\left.\vphantom{ \begin{array}{ll} 1 &; m=n\\ 0 &; m\neq n \end{array} }\right.$$

kalles en basis (et sett basistilstander), og denne dekomponeringen kalles en representasjon av tilstanden. Det er alltid flere mulige måter å velge slike basistilstander på -- det fins ingen foretrukket representasjon. Vilken representasjon man velger kommer som regel an på vilke egenskaper ved systemet man er mest interessert i.

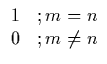
Det er viktig å legge merke til at tilstanden er noe som kjennetegner systemet som helhet, og ikke dets enkelte deler. I noen tilfeller -- når man har å gjøre med et system som består av uavhengige (ikke-vekselvirkende)⁴² deler -- kan man spalte opp tilstanden i deltilstander, som hver kan tilskrives de enkelte delene. Svært mange systemer vil det også være praktisk å betrakte som tilnærminger til slike systemer av uavhengige deler. Fra et strengt kvantemekanisk synspunkt er dette imidlertid kun å betrakte som matematiske teknikker, uten noe foretrukket fysisk innhold -- særlig ettersom tilstanden alltid kan representeres på andre måter som ikke inneholder noen slik separasjon. Ser man helt absolutt på det, kan ikke to delsystemer sies å ha noen som helst selvstendighet når de vekselvirker, eller på annet vis befinner seg i en ikke-separert tilstand.⁴³ Klarest vises dette ved at egenskaper ved de individuelle delsystemene er ubestemte i en slik sammenheng. Men som regel er dette naturligvis en upraktisk betraktningsmåte.

Siden tilstanden skal karakterisere alle systemets egenskaper, kan en forvente, i et system med mange partikler, at ikke bare partiklenes energi, impuls, innbyrdes plassering osv., men også deres type og antall, skal angis av tilstanden. I ikke-relativistisk teori kan en stort sett overse dette og ta partiklene for gitt -- bortsett fra når det gjelder fotonene, som er masseløse og dermed kan skapes i stort antall også ved lave energier.⁴⁴ I relativistisk teori (kvantefeltteorien), derimot, gjør de høye energiene som inngår at alle partikler kan oppstå og forsvinne -- og (de frie) partiklene må anses som aspekter ved systemets tilstand.

Foreløpig har jeg betraktet tilstanden som en rent abstrakt størrelse -- og tilstanden `i seg selv' er fullstendig abstrakt og nærmest et tomt begrep. Tilstanden `i seg selv' inneholder ingen direkte referanse til fysiske størrelser; heller ikke til punkter i tid og rom. (Det ligger implisitt i det at tilstanden karakteriserer hele systemet at den ikke selv kan befinne seg noe sted, verken i tida eller rommet.) En slik referanse kan kun oppnås ved å velge en bestemt representasjon av tilstanden, hvor basistilstandene er knyttet til bestemte fysiske størrelser eller egenskaper.

Enhver egenskap er i kvantemekanikken karakterisert ved en operator. En operator kan defineres som en lineær funksjon av tilstander i tilstandsrommet, som gir ut tilstander som resultat. Vi skriver F$\Psi$ = $\Psi{^\prime}$, der $\Psi$ og $\Psi{^\prime}$ er tilstander, og F er operatoren. Vi sier gjerne at operatoren virker på tilstanden $\Psi$, og at $\Psi{^\prime}$ er virkningen av operatoren. (Men dette er ikke noe som `skjer' med $\Psi$ ved et eller annet tidspunkt -- det er definisjonen av operatoren.) At den er lineær, betyr at virkningen av en operator på summen av to tilstander er lik summen av virkningene på hver av tilstandene:

F($$\alpha$$$$\Psi_{1}^{}$$ + $$\beta$$$$\Psi_{2}^{}$$) = $$\alpha$$F$$\Psi_{1}^{}$$ + $$\beta$$F$$\Psi_{2}^{}$$

Det er dette som gjør superposisjonsprinsippet relevant, siden man dermed kan knytte addisjon av tilstander til addisjon av egenskaper.

Dersom F$\Psi$ = f$\Psi$, hvor f er et tall, kalles $\Psi$ en egentilstand for F, med egenverdi f. Da har egenskapen Fden entydige verdien f i denne tilstanden. Generelt vil ikke dette være tilfelle -- da kan en ikke si at operatoren er definert innenfor tilstanden, siden F$\Psi$ inneholder tilstander som står normalt på $\Psi$. Men til enhver operator kan en finne i hvert fall noen egentilstander. Mye av arbeidet i kvantemekanikken går ut på nettopp å finne egenverdier og egentilstander.

I det generelle tilfellet kan vi definere forventningsverdi $\langle$F$\rangle$ og matriseelementer F_ab av operatoren F ved

$$\langle$$F$$\rangle_{\Psi}^{}$$ = $$\langle$$$$\Psi$$ | F$$\Psi$$$$\rangle$$ F_ab = $$\langle$$$$\Psi_{a}^{}$$ | F$$\Psi_{b}^{}$$$$\rangle$$

Dersom $\Psi$ er en egentilstand for F blir forventningsverdien til F i $\Psi$ lik egenverdien. I en gitt representasjon vil en operator være fullstendig karakterisert ved matriseelementene av operatoren mellom basistilstandene -- kjenner en alle disse, er virkningen av operatoren på en vilken som helst tilstand gitt.

En målbar størrelse (som energi, ladning, posisjon osv.) er karakterisert ved en reell operator, dvs. at $\langle$$\Phi$ | F$\Psi$$\rangle$ = $\langle$F$\Phi$ | $\Psi$$\rangle$ = $\langle$$\Phi$ | F | $\Psi$$\rangle$ for alle $\Phi$,$\Psi$. Disse vil alltid ha reelle egenverdier (og forventningsverdier).

Når vi måler en størrelse, vil vi aldri få andre verdier enn egenverdiene for den tilsvarende operatoren. Dette gjelder selv om systemet befinner seg i en tilstand som ikke er egentilstand for operatoren. Dette henger sammen med at tilstanden alltid kan skrives som en lineærkombinasjon av egentilstander for operatoren, og at operatoren virker på disse separat og gir ut egenverdien for hver av disse. I tilstander som ikke er egentilstander kan vi dermed ikke forutsi i hvert enkelt tilfelle resultatet av en måling, siden størrelsen ikke har noen bestemt verdi i denne tilstanden -- den er prinsipielt ubestemt. Dette, og at målinger (generelt) ikke kan gi alle mulige verdier, er noe som som skiller kvantemekanikken klart fra klassisk fysikk. Det siste er det som kan betegnes med at mange størrelser er kvantiserte (og bryter med prinsippet om at `naturen gjør ikke noen sprang').⁴⁵

Siden målbare størrelser er knyttet til reelle operatorer, vil alle mulige resultater av målinger være reelle tall. Egentilstandene for målbare størrelser har også de egenskapene som kreves av basistilstander. Altså, dersom F representerer en målbar størrelse, vil enhver tilstand kunne skrives

 | $$\Psi$$$$\rangle$$ = $$\sum_{n}^{}$$$$\alpha_{n}^{}$$ | f_n$$\rangle$$ med  F | f_n$$\rangle$$ = f_n | f_n$$\rangle$$

hvor⁴⁶

$$\langle$$f_n | f_m$$\rangle$$ = $$\delta_{nm}^{}$$

Dersom $\Psi$ er en fysisk tilstand, er

$$\sum_{n}^{}$$|$$\alpha_{n}^{}$$|² = 1 og  $$\langle$$F$$\rangle_{\Psi}^{}$$ = $$\sum_{n}^{}$$f_n|$$\alpha_{n}^{}$$|²

Ved måling kan F anta en vilken som helst av verdiene f₁, f₂,..., mens |$\alpha_{n}^{}$|² angir sannsynligheten for hvert slikt resultat. Man ser raskt at alle krav som stilles til sannsynligheter er oppfylt. $\alpha_{n}^{}$ kalles gjerne sannsynlighetsamplituder. Denne tilordningen av utviklingskoeffisientene til fordelingen av resultatene i et stort antall identisk preparerte forsøk, er Borns statistiske tolkning av kvantemekanikken.

Vi kan altså benytte oss av egentilstandene for målbare størrelser til å lage representasjoner av tilstandene. Én slik representasjon -- posisjonsrepresentasjonen -- får en ved å utvikle tilstanden i egentilstander |$\vec{r'}\,$ > av posisjonsvektoren $\vec{r}\,$ til en partikkel (vi tenker oss nå at systemet består av én partikkel). I en slik egentilstand befinner denne partikkelen seg med sikkerhet i posisjonen $\vec{r'}\,$. En generell tilstand vil da være⁴⁷

 | $$\Psi$$$$\rangle$$ = $$\int$$$$\psi$$($$\vec{r}\,$$) | $$\vec{r}\,$$$$\rangle$$d³r

der $\psi$($\vec{r}\,$) = $\langle$$\vec{r}\,$ | $\Psi$$\rangle$ er Schrödingers bølgefunksjon, som karakteriserer tilstanden i denne representasjonen. |$\psi$($\vec{r}\,$)|² angir sannsynligheten for at partikkelen vil bli funnet i posisjonen $\vec{r}\,$ ved en måling.

En annen mye brukt representasjon av tilstanden er energirepresentasjonen. Ofte regner vi et kvantemekanisk problem som løst dersom vi greier å finne energiegenverdiene til systemet (og andre karakteristika ved energiegentilstandene). Dette har bl.a. sammenheng med at energien er en bevart størrelse, slik at et isolert system som på ett tidspunkt befinner seg i en energiegentilstand, vil gjøre det for all tid. (Eller sagt på en annen måte: En tilstand som er egentilstand for energien ved ett tidspunkt, vil også være egentilstand for energien ved ethvert annet tidspunkt). Eksempler på energiegentilstander er stasjonære tilstander i atomer og partikler med en gitt impuls i kvantefeltteorien.

At en gitt størrelse ikke kan gis noen entydig verdi i enhver tilstand betyr også at to størrelser ikke bestandig kan gis entydige verdier (måles eksakt) samtidig eller i samme tilstand: En egentilstand for den ene behøver ikke å være en egentilstand for den andre. Tvert imot: Det finnes størrelser som ikke har noen felles egentilstander. Disse kan altså aldri gis presise verdier samtidig. Andre størrelser kan ha noen felles egentilstander, og kan altså i enkelte, men ikke alle tilfelle gis presise verdier samtidig. Jeg vil kalle alle slike størrelser inkompatible. Dersom to størrelser alltid skal kunne gis presise verdier samtidig, altså dersom alle egentilstander  | n$\rangle$er felles, følger at

$$\Psi \rangle \sum_{n}^{} \alpha_{n}^{} \rangle \sum_{n}^{} \alpha_{n}^{} \rangle$$ =

$$\sum_{n}^{} \alpha_{n}^{} \rangle \sum_{n}^{} \alpha_{n}^{} \rangle$$ =

$$\Psi \rangle$$ =

for alle tilstander  | $\Psi$$\rangle$. Dette er både en nødvendig og tilstrekkelig betingelse for at størrelsene skal være kompatible. Det vil si at

[F, G]$$\;\stackrel{\rm def}{=}\;$$FG - GF = 0

Operatoren [F,G] kalles kommutatoren mellom F og G. Dersom denne ikke er lik null, er de to størrelsene inkompatible.

Vi kan ofte uttrykke kommutatoren mellom to operatorer ved hjelp av kjente operatorer -- helt uten referanse til vilken representasjon vi har valgt. Slike kommutatorrelasjoner danner det mest generelle utgangspunktet for beskrivelsen av et system -- mesteparten av fysikken i systemet kan uttrykkes ved hjelp av kommutatorrelasjoner. Blant annet kan dynamikken i kvantemekaniske systemer uttrykkes som kommutatorrelasjoner mellom kjente størrelser og deres deriverte. En kan også si at et system er gitt ved kommutatorrelasjonene mellom de operatorene som karakteriserer systemet. De definerer tilstandsrommets `form': Hva slags tilstander som er tillatte og forbudte. Ofte kan en også hente ut informasjon om mulige egenverdier nærmest direkte fra kommutatorrelasjonene.⁴⁸

Uttrykket for kommutatoren [F,G] kan fortelle om fordelingen av egenverdiene for G i en tilstand med gitt fordeling av F's egenverdier. Dermed får vi uskarphetsrelasjoner -- nedre grenser for hvor nøyaktig man kan angi verdier for inkompatible størrelser samtidig. Den generelle formen er, dersom

[F, G] = i$$\hbar$$K$$\mbox{\hspace*{10mm}hvor $K$\space er en reell operator,}$$

så er

$$\Delta$$F$$\Delta$$G $$\geq$$ $${\frac{\hbar}{2}}$$|$$\langle$$K$$\rangle$$|

hvor $\Delta$F ($\Delta$G) er spredningen (uskarpheten) i Fs (Gs) egenverdier i den gitte tilstanden.⁴⁹ For impuls og posisjon til samme partikkel får vi, siden [x, p] = - i$\hbar$

$$\Delta$$x$$\Delta$$p $$\geq$$ $${\frac{\hbar}{2}}$$

Dette er den opprinnelige Heisenbergs uskarphetsrelasjon.

I kvantefeltteorien snakker en ikke lenger om partiklenes posisjoner som operatorer, slik en gjør i den `tradisjonelle' kvantemekanikken. Siden partikkeltallet kan variere, er det vanskelig å få en slik størrelse til å bli veldefinert. Dessuten ville det bryte med kravet til relativistisk invarians, ettersom tida nødvendigvis må være en parameter: Forutsetningen for at det skal gi mening å snakke om en partikkels posisjon som en målbar størrelse (eller om målbare størrelser i det hele tatt) er at vi underforstår at det er snakk om posisjonen (eller energien eller dreieimpulsen eller...) ved en tid t. En måling må nødvendigvis foretas på ett eller annet tidspunkt (eller egentlig: over et visst tidsrom). Denne betraktningsmåten er imidlertid åpenbart ikke tilfredsstillende i en relativistisk teori, hvor tid- og romkoordinater bør behandles på `like fot'.⁵⁰

Dette problemet løses ved å gjøre også romkoordinatene til parametre. Et kvantefelt er akkurat som et klassisk felt, bortsett fra at `verdiene' i hvert punkt ikke er tall, men operatorer. Systemet karakteriseres altså ved et sett av feltoperatorer, som er definert overalt i tid-rommet. Det er ikke noe nødvendig krav at operatorene skal være reelle -- de fleste feltene er det ikke. Lagrangetettheten og feltligningene beskriver nå sammenhenger mellom operatorer. I tillegg har en kommutatorrelasjoner mellom feltene, som bl.a. gir opphav til de typiske kvantemekaniske uskarphetene eller fluktuasjonene.

Et viktig krav som stilles til feltoperatorene er mikrokausalitet: Dersom det ikke kan gå noe signal mellom to punkter, altså dersom avstanden mellom dem er rom-lik, kan heller ikke feltene i disse punktene måtte `ta hensyn til' hverandre -- feltene må være separert, og alle målbare størrelser som kan konstrueres fra feltoperatorene i de to punktene må være kompatible. En måling det ene stedet kan ikke ha noe å si for en måling det andre stedet (dersom ikke systemet på forhånd er preparert i en tilstand som korrelerer verdiene i de to punktene). Matematisk uttrykt:

(x - y)² = 0 $$\Rightarrow$$ [A(x), B(y)] = 0

der (x - y)² er den relativistiske avstanden mellom punktene x og y, og A(x), B(y) er målbare (reelle) størrelser konstruert fra feltoperatorene.

Bare ett av feltene har en klassisk analog: det elektromagnetiske feltet. Alle feltene svarer til en bestemt partikkeltype, og en kan fra feltoperatorene konstruere operatorer for energi- og impulstetthet, ladningstetthet osv. for denne partikkeltypen. Partiklene dukker opp som tilstander med veldefinerte verdier for masse, ladning og andre kvantetall. Det er imidlertid ingen referanse til posisjonen til en individuell partikkel. Dette er, som vi skal se, som det skal være.

   
Transformasjoner og symmetrier

En transformasjon (av det aller mest generelle slaget) er i kvantemekanikken et skifte av representasjon:

 | $$\Psi$$$$\rangle$$ = $$\sum_{n}^{}$$$$\alpha_{n}^{}$$ | f_n$$\rangle$$ = $$\sum_{m}^{}$$$$\beta_{m}^{}$$ | g_m$$\rangle$$

Transformasjonen kan karakteriseres ved en transformasjonsmatrise S_mn,⁵¹ som relaterer utviklingskoeffisientene til hverandre:

$$\beta_{m}^{}$$ = $$\sum_{n}^{}$$S_mn$$\alpha_{n}^{}$$ med  S_mn = $$\langle$$g_m | f_n$$\rangle$$

En svært viktig klasse transformasjoner er koordinattransformasjoner, hvor vi ser på systemet fra et koordinatsystem som er dreid, forskjøvet eller på annen måte transformert i forhold til det opprinnelige. Eksempler på slike er de klassiske symmetritransformasjonene. Disse er en delmengde av en større gruppe transformasjoner hvor de operatorene som danner basis for representasjonene har det samme spektrum av egenverdier. Dermed kan også koordinattransformasjoner i kvantefeltteorien regnes med, selv om romkoordinatene ikke er operatorer: De reelle operatorene som konstrueres fra feltoperatorene $\Phi$(x') har de samme egenverdiene som de som konstrueres fra $\Phi$(x). For alle slike transformasjoner gjelder at vi kan bilde dem på to måter:

1. Passiv: Tilstanden (systemet) ligger fast, men vi ser det fra en annen synsvinkel. Vi kan uttrykke operatoren G, som danner basis for den nye representasjonen, ved hjelp av F, som danner basis for den gamle. F.eks.: F = x ; G = x + a-- translasjon. Uttrykket (matriseelementene) for alle operatorer blir forandret til A'_mn = $\sum_{k,l}^{}$S_mkA_kl(S^-1)_kn.

2. Aktiv: Vi transformerer tilstanden (f.eks.: $\psi$(x) $\rightarrow$ $\psi$(x + a)). Her kan vi se på transformasjonsmatrisen som en operator som virker i tilstandsrommet:

S$$\Psi$$ = S$$\sum_{n}^{}$$$$\alpha_{n}^{}$$ | n$$\rangle$$ = $$\Psi{^\prime}$$ = $$\sum_{n}^{}$$$$\beta_{n}^{}$$ | n$$\rangle$$

Denne operatoren er igjen veldefinert uavhengig av representasjonen. En vilkårlig operator vil generelt ikke ha samme virkning på den transformerte tilstanden som på den opprinnelige, men vi kan definere en transformert operator A' = SAS^-1, som har de samme matriseelementene. Den transformerte operatoren er den samme som den opprinnelige dersom den kommuterer med transformasjonsoperatoren: [A, S] = 0.

Ofte betrakter vi en gruppe likeartede transformasjoner (f.eks. gruppen av alle mulige romtranslasjoner) under ett. Da kan vi uttrykke transformasjonen ved hjelp av en parameter $\alpha$

Identiske partikler

I kvantemekanikken betrakter man ofte systemer bestående av flere identiske partikler (partikler uten noen individuerende kjennetegn, f.eks. elektroner i et atom). Man kan i et slikt system definere en operasjon hvor en bytter om alle koordinater eller kvantetall til to (eller flere) partikler, eller (noe som er ekvivalent) bytter om to partikler. Dersom partiklene (som vi kan kalle `partikkel 1' og `partikkel 2') er virkelig identiske, kan vi ikke se forskjellen på tilstanden $\Psi$(1, 2) `før' og $\Psi$(2, 1) `etter' denne operasjonen -- f.eks. må alle operatorer ha samme forventningsverdi. Da må $\Psi$(1, 2) være en konstant ganger $\Psi$(2, 1), og siden vi åpenbart må få tilbake samme tilstand når vi gjentar operasjonen, betyr det at $\Psi$(2, 1) = $\pm$ $\Psi$(1, 2).⁵²

Partikler hvor $\Psi$(2, 1) = - $\Psi$(1, 2) kalles fermioner; partikler hvor $\Psi$(2, 1) = $\Psi$(1, 2) kalles bosoner. Dette kan også generaliseres til å gjelde systemer med flere enn to partikler: Tilstanden til et system vil alltid være symmetrisk ved ombytte av to identiske bosoner, og antisymmetrisk ved ombytte av to identiske fermioner. Vi ser altså at vi får betingelser på tilstanden som utelukkende skyldes det faktum at partiklene er identiske.

Dersom partiklene ikke vekselvirker, betyr det at vi kan fastsette (måle) alle kvantetall for alle partiklene samtidig. For fermioner ser vi da at to partikler aldri kan ha det samme settet med kvantetall, siden vi da ville få at $\Psi$(1, 2) = $\Psi$(2, 1) = - $\Psi$(1, 2) -- som er umulig for en fysisk tilstand. Dette er Paulis utelukkelsesprinsipp: To fermioner kan aldri befinne seg i samme (enpartikkel)tilstand samtidig.

Dette er nødvendig, men ikke tilstrekkelig for å være fermion. For å se det, er det nok å merke seg at dersom partikkel 1 befinner seg i enpartikkeltilstanden $\Psi_{a}^{}$ (har kvantetallene a), mens partikkel 2 befinner seg i tilstanden $\Psi_{b}^{}$, vil totaltilstanden kunne skrives $\Psi$(1, 2) = $\Psi_{a}^{}$(1)$\Psi_{b}^{}$(2). Denne tilstanden oppfyller ikke symmetrikravene verken for fermioner eller bosoner.

Derimot vil tilstandene

$$\Psi_{-}^{} {\frac{1}{\sqrt{2}}} \Psi_{a}^{} \Psi_{b}^{} \Psi_{b}^{} \Psi_{a}^{}$$ =

$$\Psi_{+}^{} {\frac{1}{\sqrt{2}}} \Psi_{a}^{} \Psi_{b}^{} \Psi_{b}^{} \Psi_{a}^{}$$ =

oppfylle kravene for henholdsvis fermioner og bosoner. Dersom partiklene 1 og 2 er fermioner, vil $\Psi_{-}^{}$ være en tillatt tilstand for systemet av de to partiklene, mens $\Psi_{+}^{}$ vil være en tillatt tilstand dersom de to partiklene er bosoner. Men dette betyr at partiklene ikke kan ha sine kvantetall uavhengig av hverandre -- de er ikke-vekselvirkende (i hvert fall ikke vekselvirkende i vanlig forstand), men ikke uavhengige. Tilstandene kan ikke separeres i en del som bare har med den ene partikkelen å gjøre og en annen del som bare angår den andre; en forandring av den enes tilstand vil også være en forandring av den andres tilstand. Dette gir målbare effekter: Forventningsverdien av en størrelse A i disse tilstandene vil inneholde et `interferensledd'

$$\mp$$ Re($$\Psi_{a}^{}$$$$\Psi_{b}^{}$$, A$$\Psi_{b}^{}$$$$\Psi_{a}^{}$$)

som uttrykker at systemet `er' i begge tilstandene $\Psi_{a}^{}$$\Psi_{b}^{}$ og $\Psi_{b}^{}$$\Psi_{a}^{}$. Dersom A er produktet av to størrelser som har med hver sin partikkel å gjøre: A = A<sub>1</sub>(1)A<sub>2</sub>(2) (f.eks.: spinnet i z-retningen for partikkel 1 og spinnet i en litt annen retning for partikkel 2), vil $\langle$A$\rangle$ uttrykke en korrelasjon mellom verdiene av A<sub>1</sub> for partikkel 1 og A<sub>2</sub> for partikkel 2. Denne korrelasjonen vil også inneholde et slikt `merkelig' ledd. Partiklenes posisjoner blir også korrelert på denne måten -- med det resultatet at bosoner liker hverandre, mens fermioner avskyr hverandre: Sannsynligheten for å finne to fermioner veldig nær hverandre er liten, mens den er betydelig større enn `forventet' for bosoner.

Vi kan også legge merke til at dette gjelder uansett hvor langt fra hverandre de to partiklene er: Tilstandens symmetri er helt uavhengig av avstander (selv om størrelsen på korrelasjonsleddet avtar med avstanden). Det vil si at vi faktisk er korrelert med noe i Andromeda-tåken (eller bak månen, viss vi vil være litt mer jordnære). Dette, og lignende fenomener, er en del av essensen i Bells teorem, som fastslår at lokale, realistiske teorier er inkompatible med kvantemekanikken.

Et viktig resultat i kvantestatistikken er Wigners `summasjonsformel', som sier at der en ansamling av flere fermioner kan oppfattes som en udelelig enhet (som f.eks. i en atomkjerne), oppfører den seg som et boson dersom den består av et like antall fermioner, og som et fermion dersom den består av et odde antall. Dette ser en direkte ved å legge merke til at ombytte av to enheter av et like antall fermioner, er lik et like antall fermionombytter, som gir et like antall fortegnsskift, altså ingen netto forandring av tilstanden. Tilsvarende får vi for et odde antall. Eller man kan benytte seg av det faktum (som opprinnelig var en empirisk oppdagelse) at alle partikler med halvtallig spinn er fermioner, mens alle partikler med heltallig spinn er bosoner. Ved å benytte reglene for addisjon av dreieimpuls, ser en at aggregater av et like antall partikler med halvtallig spinn har heltallig `indre dreieimpuls' (som i denne sammenhengen kan betraktes som aggregatets spinn), mens et odde antall gir halvtallig `indre dreieimpuls'. (Banedreieimpulsen er bestandig heltallig, så den spiller forsåvidt ingen rolle.)

I kvantefeltteorien faller alle disse resultatene rett ut av grunnsetningene, uten noen tilleggsantakelser: Feltoperatoren $\Phi$kan skrives som sammensatt (en lineærkombinasjon)⁵³ av en rekke operatorer a(p), a^$\dag$(p) -- en for hver mulig verdi av en parameter $\vec{p}\,$. Når man konstruerer en energi-impulstetthet og en energioperator H ut fra Lagrangetettheten, og krever at operatorene skal oppfylle Heisenbergs bevegelsesligning

i$$\hbar$$$${\frac{\partial\Phi}{\partial t}}$$ = [$$\Phi$$, H]

(eller andre, ekvivalente kvantiseringsbetingelser), kan dette skrives om til kommutatorrelasjoner mellom a-ene og a^$\dag$-ene, slik at de fremstår som hhv. ødeleggelsesoperatorer og skapelsesoperatorer:

Med en definisjon av vakuum  | 0$\rangle$ og de fysiske operatorene for totalenergi H og totalimpuls $\vec{P}\,$, slik at bl.a. H | 0$\rangle$ = 0, $\vec{P}\,$ | 0$\rangle$ = 0, vil a^$\dag$(p) | 0$\rangle$ bli egentilstander av H og $\vec{P}\,$ med egenverdier hhv. E($\vec{p}\,$) = $\sqrt{\vec{p}^2c^2+m^2c^4}$ og $\vec{p}\,$. Den totale energien og impulsen er generelt uttrykt ved

H = $$\int$$d³pE($$\vec{p}\,$$) a(p)a(p) $$\vec{P}\,$$ = $$\int$$d³p $$\vec{p}\,$$ a(p)a(p)

 Vi kan tolke dette som at antallsoperatoren n(p) = a^$\dag$(p)a(p) betegner antallet partikler med impuls $\vec{p}\,$ og energi E($\vec{p}\,$), og at tilstanden  | p$\rangle$ = a^$\dag$(p) | 0$\rangle$ er en partikkel -- a^$\dag$(p) skaper en partikkel med skarpt definert energi og impuls. Vi finner også at a(p) | p$\rangle$ =  | 0$\rangle$: a(p) ødelegger en partikkel. Vi kan definere en totalantallsoperator

N = $$\int$$d³p a(p)a(p)

som har heltallige egenverdier. En egentilstand for N med egenverdi n er n partikler. Disse behøver ikke å ha skarpt definert energi og impuls, men kan være `blandingstilstander'.

Denne formalismen gjør det umulig å fastholde noen individualitet for partiklene. At vi ser tilstandene som partikler (eller overlagringer av partikler) er bare én mulig representasjon. Det er fullt tillatt med tilstander som er overlagringer av tilstander med forskjellige partikkeltall. Disse tilstandene kan også være av fysisk interesse: For eksempel er egentilstander for de elektriske og magnetiske feltene $\vec{E}\,$ og $\vec{B}\,$tilstander hvor partikkeltallet er ubestemt -- elektromagnetiske feltstyrker og fotontall er inkompatible størrelser. Og der en har et bestemt antall partikler, er det bare i grensetilfeller at en kan si noe om vilken som er vilken, ved at de f.eks. er romlig separert. Tilstanden gir ikke enkeltpartikkelen noen særstatus eller `personlighet', og fremfor alt forsikrer formalismen at partikler av samme slag er fullstendig identiske -- de utgår alle av det samme feltet. Tilstandene er tilstander av feltene, og er ikke tilordnet individuelle partikler, men i høyden et antall.

Skillet mellom fermioner og bosoner kommer frem i den måten kvantisering foregår på. Kravene om mikrokausalitet og at det finnes et laveste energinivå gjør at man for felt med heltallig spinn (skalar-, vektor- eller tensorfelt) må ha blant annet (essensielt)⁵⁴

[a(p), a(p')] = [a(p), a(p')] = 0

mens man for felt med halvtallig spinn (spinorfelt) må ha

{a(p), a(p')} = {a(p), a(p')} = 0 der  {a, b}$$\;\stackrel{def}{=}\;$$ab + ba

Det første gir opphav til Bose-Einstein-statistikk (bosoner), mens det andre gir opphav til Fermi-Dirac-statistikk (fermioner). Spesielt ser vi at Pauli-prinsippet er oppfylt: Prøver en å skape en tilstand med to partikler med samme energi og impuls, får en

(a(p))² | $$\Psi$$$$\rangle$$ = $${\textstyle\frac{1}{2}}$${a(p), a(p)} | $$\Psi$$$$\rangle$$ = 0

Dette spinn-statistikk-teoremet er bevist helt generelt innen rammen av aksiomatisk feltteori.

Ladete partikler (eller partikler som har en antipartikkel) representeres ved et felt $\Phi$ som ikke er reelt. Det har da et tilhørende konjugert felt $\Phi^{\dag}_{}$, og to sett med skapelses- og ødeleggelsesoperatorer: a, a^$\dag$ ødelegger eller skaper partikler, mens b, b^$\dag$ ødelegger eller skaper antipartikler (partikler med motsatt ladning). Feltet $\Phi$ kan skrives vha a- og b^$\dag$-operatorer, og vil altså ødelegge en partikkel eller skape en antipartikkel. $\Phi^{\dag}_{}$ inneholder b- og a^$\dag$-operatorer, og vil altså skape en partikkel eller ødelegge en antipartikkel.

Vekselvirkninger

Dersom to delsystemer ikke vekselvirker, vil totalsystemets energi kunne skrives som en sum av to ledd som hver bare avhenger av det ene delsystemet, og delsystemene vil utvikle seg helt uavhengig av hverandre. Vekselvirkningen beskrives da ved et ledd som avhenger av begge delsystemene, og som ikke kan spaltes opp. Det enkleste eksemplet er kanskje vekselvirkningen mellom to massive legemer i klassisk (Newtonsk) teori:

E = $${\textstyle\frac{1}{2}}$$m₁v₁² + $${\textstyle\frac{1}{2}}$$m₂v₂² - G$${\frac{m_1m_2}{\vert\vec r_1 - \vec r_2\vert}}$$

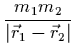
Her ser en hvor felt-tanken kommer fra: Dette kan betraktes på en alternativ måte -- nemlig at legeme 1 setter opp et felt rundt seg, som er proporsjonalt med massen m₁ og omvendt proporsjonalt med avstanden fra legemet. Det andre legemet får så et tillegg i energien på grunn av en kobling til dette feltet, som avhenger av legemets masse og av feltets styrke. Dersom vi lar feltet bre seg ut med en endelig hastighet fra det ene legemet til det andre, ser vi at energien også blir avhengig av om feltet har `rukket' å nå frem til det andre legemet. Vi kan også la feltet bære med seg sin egen energi, som er avhengig bare av feltstyrken.

Dette er situasjonen i klassiske, dualistiske teorier -- det typiske (og eneste?) eksemplet er klassisk elektrodynamikk: Både de ladete partiklene og feltet har sin intrinsikke bevegelse og sin egen energi; i tillegg kommer koblingen mellom dem, som gjør at de modifiserer hverandre gjensidig.

Alt dette kan skrives om og innbakes i en Lagrangeteori, hvor vekselvirkningen opptrer som tillegg til de `frie' Lagrangefunksjonene og Lagrangetetthetene. I en ikke-dualistisk feltteori ses partiklene kun som `fortetninger' av feltene, hvert felt kan ses som et delsystem, og vekselvirkningen manifesterer seg gjennom et lokalt tillegg i Lagrangetettheten:

$$\cal$$L($$\Phi_{1}^{}$$,$$\Phi_{2}^{}$$) = $$\cal$$L₁($$\Phi_{1}^{}$$) + $$\cal$$L₂($$\Phi_{2}^{}$$) + $$\cal$$L_vv($$\Phi_{1}^{}$$,$$\Phi_{2}^{}$$)

I behandlingen av partikler i forrige avsnitt så jeg bort fra vekselvirkningen mellom dem. Det viser seg at vekselvirkninger har innflytelse både på partiklers stabilitet og på hvor meningsfylt det er å snakke om partikler. Partiklene i forrige avsnitt er tilstander for systemet av frie felt, og beveger seg fritt. Når feltene eller partiklene vekselvirker, blir bildet forkludret. Heisenbergs bevegelsesligning (eller hva vi nå bruker som kvantiseringsbetingelse) ser annerledes ut, og kommutatorrelasjonene blir forskjellige. Det kan bli vanskelig å kjenne igjen operatorene, energiegentilstander er ikke nødvendigvis egentilstander for antallsoperatorene -- tilstandene ser i det hele tatt annerledes ut. Partiklene mister altså enda mer av sin identitet. Og tidsutviklingen er naturligvis en annen (ellers ville det ikke være noen vits i å snakke om en vekselvirkning).

Situasjonen er ikke fullt så håpløs som det her kan se ut til. Man kan nemlig velge en representasjon av systemets totaltilstand -- kalt vekselvirkningsbildet -- som er slik at (uttrykket for) tilstandene hadde vært tidsuavhengig dersom vekselvirkningen var null, og kommutatorrelasjonene for feltene er de samme som for de frie feltene, som vi kjenner egenskapene til. Dette er altså en tredje måte å se tidsutviklingstransformasjonen på, i tillegg til Heisenbergbildet og Schrödingerbildet som er beskrevet i avsnitt 2.3.3. På denne måten kan en ta utgangspunkt i løsningene til et kjent problem når en skal løse det mer kompliserte vekselvirkningsproblemet.

Vekselvirkningsproblemet kan deles i to hovedgrupper:

1. Bundne tilstander. Her er det snakk om å finne stabile tilstander med en definitt energi (som er lavere enn energien for frie partikler), med en begrenset og konstant romlig utstrekning (dvs. at området hvor energitettheten i middel er merkbart forskjellig fra null er begrenset og konstant). Eksempler på slike tilstander er atomer (bundne tilstander av en kjerne og ett eller flere elektroner) og hadroner (bundne tilstander av kvarker og gluoner). Det skulle ikke være noe i kvantefeltteoriens begrepsapparat som gjør det prinsipielt umulig å beregne dette; imidlertid er det et faktum at man aldri har lykkes i å utvikle rigorøse metoder til å takle disse problemene. Det som vanligvis gjøres, er å transformere problemet til et ikke-relativistisk potensialproblem med fast partikkeltall, som man kan løse ved hjelp av kjente metoder. Deretter kan kvantefeltteori tas i bruk for å beregne relativistiske korreksjoner, som forhåpentligvis er små. Gyldighetsområdet til en slik tilnærming er ikke kjent med sikkerhet.

Korreksjonene til en kjent (tilnærmet) løsning beregnes ved å ta i bruk vekselvirkningsbildet: Det kjente, bundne systemet regnes for anledningen som et `fritt' (kjent) delsystem, og korreksjonsleddene regnes som `vekselvirkning'. Dersom korreksjonsleddene er små, kan en så bruke perturbasjonsmetoder.

2. Spredningsproblemer. Begrepet spredning bruker jeg her i ordets videste betydning: Vekselvirkningen er merkbart forskjellig fra null kun over et endelig tidsintervall; utenfor dette tidsintervallet kan delsystemene regnes som frie (og uavhengige). Spesielt er dette tilfelle der flere partikler nærmer seg hverandre, reagerer, og reaksjonsproduktene siden fjerner seg fra hverandre. Slike problemer har kvantefeltteorien vist seg særdeles velegnet til å løse.

I vekselvirkningsbildet kan vi regne som om feltene var frie. Videre vet vi at tilstandene lenge før og lenge etter vekselvirkningen (de asymptotiske tilstandene) er frie partikler, og disse kan tas som utgangspunkt for beregningen. Vi er dessuten sjelden interessert i detaljene i vekselvirkningen, bare i sannsynligheten for overganger mellom ulike asymptotiske tilstander. Disse sannsynlighetene er uttrykt gjennom S-matrisen, som er den asymptotiske formen på tidsutviklingsoperatoren (operatoren for tidsutviklingstransformasjonen) i vekselvirkningsbildet: Med

$$\Psi$$(t) = U(t, t₀)$$\Psi$$(t₀)

er

S$$\;\stackrel{\rm def}{=}\;$$$$\lim_{t \rightarrow\infty,t_0 \rightarrow-\infty}^{}$$U(t, t₀)

Man kan skrive opp et eksplisitt uttrykk for S-matrisen ved hjelp av vekselvirkningsleddet i Lagrangetettheten:

S = e^{(i/$\hbar$)$\int$$\cal$L_vv(x)d4x}

Denne operatorligningen er svært vanskelig å løse eksakt. Dersom $\cal$L_vv kan regnes for å være liten, kan man utvikle eksponensialfunksjonen i en potensrekke:

e^x = 1 + x + x²/2! + x³/3! +..., dvs.

S = 1 + (i/$$\hbar$$)$$\int$$$$\cal$$L_vv(x)d⁴x + $${\textstyle\frac{1}{2}}$$(i/$$\hbar$$)²$$\int$$$$\cal$$L_vv(x₁)d⁴x₁$$\int$$$$\cal$$L_vv(x₂)d⁴x₂ +...

og anta at de høyere ordens leddene gir små bidrag til S-matrisen.⁵⁵

Dermed kan prosessene ses på som sammensatt av `elementære vekselvirkninger' (elementære prosesser) gitt ved $\cal$L_vv, som kan finne sted (eller finner sted) når som helst i tid og hvor som helst i rommet, og kan foregå en eller flere ganger. Prosesser som er sammensatt av flere elementære prosesser er mindre sannsynlige enn de som er sammensatt av færre. Det totale S-matriseelementet for en overgang mellom to gitte tilstander finnes ved å summere opp bidraget fra alle mulige (usammensatte og sammensatte) prosesser som bringer den ene tilstanden over i den andre. Overgangssannsynligheten er (proporsjonal med) absoluttkvadratet av S-matriseelementet.

Nå kan det være på sin plass å si noe om formen vekselvirkningen kan ha. Relativistisk invarians krever at alle vekselvirkningsledd hvor det inngår fermionfelt (spinn 1/2-felt) må ha formen⁵⁶

$$\cal$$L_vv(x) $$\sim$$ $$\Psi_{a}^{\dag }$$(x)$$\Phi$$(x)$$\Psi_{b}^{}$$(x)

hvor $\Psi_{a}^{}$ og $\Psi_{b}^{}$ nå er fermionfelt (bokstaven $\Psi$ brukes av historiske grunner) og $\Phi$ er et bosonfelt. Dersom vi nå sier at det totale antallet fermioner er lik det totale antall partikler minus det totale antall antipartikler, finner vi at det totale fermiontallet er bevart: $\Psi_{b}^{}$ må enten ødelegge en partikkel eller skape en antipartikkel, og samtidig må $\Psi_{a}^{\dag}$ enten skape en partikkel eller ødelegge en antipartikkel. Samtidig blir et boson enten skapt (emittert) eller ødelagt (absorbert); bosonet virker som en `formidler' av prosessen.

I kvanteelektrodynamikken er dette de eneste mulige vekselvirkningene. I de ikke-abelske gauge-teoriene forekommer også `selv-vekselvirkninger' hvor bosonfeltene (gauge-feltene) kobler til hverandre, i ledd av formen $\Phi_{1}^{}$$\Phi_{2}^{}$$\Phi_{3}^{}$ og $\Phi_{1}^{}$$\Phi_{2}^{}$$\Phi_{3}^{}$$\Phi_{4}^{}$ (feltene kan være like eller forskjellige).

Feynman har funnet opp en metode for å representere elementærprosessene ved hjelp av enkle diagrammer, hvor hvert element i diagrammene er knyttet til en faktor i S-matriseelementet. På denne måten får man samtidig en visualisering av prosessene og enkle regler for beregningen. Diagrammene er rom-tid-fremstillinger med en tidsakse (som vanligvis tegnes oppover) og en `romakse' (som skal sammenfatte alle tre romkoordinatene og som tegnes horisontalt). Partikkeltilstandene representeres ved linjer som skal forestille partikkelens `verdenslinje': dens posisjon i rommet som funksjon av tida.

Vi har de følgende enkle diagramelementene:

fermion	antifermion
(spinn-1/2 partikkel)

foton	gluon	andre bosoner
		( W$\pm$, Z0, Higgs m.fl.)

vekselvirkninger

På grunn av impuls- og energibevarelse kan ingen av de elementære vekselvirkningene foregå alene -- man må ha minst to for å få en fysisk prosess. Noen enkle fysiske prosesser er illustrert i figur 3.

  

Figure 3: Noen enkle prosesser

Et problem som dukker opp med vekselvirkningen er å definere hva en fri partikkel er. Enhver partikkel kan nemlig når som helst vekselvirke med seg selv -- dvs. at vi kan ha prosesser hvor én partikkel kommer inn og én partikkel, av samme slag og med samme energi og impuls, går ut. Et elektron vil f.eks. fra tid til annen emittere et foton for straks etter å absorbere det (dvs. at man går over fra en `ren' elektrontilstand til en elektron-foton-tilstand og tilbake). På samme måte vil et nøytrino fra tid til annen være `dissosiert' i et elektron og et W-boson, mens et foton vil være `dissosiert' i et fermion-antifermion-par. Man kan på ingen måte se på en partikkel om systemet har `vært innom' en eller flere slike tilstander, eller evt. hvor mange ganger det har skjedd -- partiklene har ingen hukommelse. Derimot har det klare konsekvenser for partiklenes propagering og deres vekselvirkningsegenskaper. For å få egenskapene til det elektronet vi kan observere, må vi legge sammen bidrag fra alle mulige selvvekselvirkningsprosesser (som i figur 4)

  

Figure 4: Elektronets selvvekselvirkning

og erstatte massen for det `nakne' elektronet med massen for det `påkledte' elektronet i figuren. På tilsvarende vis blir elementærladningen endret ved at man `kler på' fotonet. Dette kalles renormalisering. Den observerte ladningen og massen for partiklene er altså forskjellig fra de størrelsene som inngår i grunnligningene, og som ville vært partiklenes ladning og masse dersom det ikke hadde vært noen vekselvirkninger (men da kunne man heller ikke hatt noen mulighet til å observere dem). Denne forskjellen er faktisk uendelig!

   
Veiintegralformalismen

Denne fremstillingen ville ikke være fullstendig uten at jeg sa noe om Feynmans veiintegralformalisme. Strengt tatt tilhører ikke denne formalismen kvantefeltteorien i begrepsmessig forstand, og derfor har jeg spart den til nå, men matematisk sett er den ekvivalent. Jeg gjør det ganske kort; Feynman har selv laget en fremstilling av teorien beregnet på den helt uinnvidde i [10]. Hans artikler [33,34] hvor han først presenterte formalismen er også leselige for en `alminnelig' fysiker.

Formalismen tar utgangspunkt i partiklene og deres baner i tid og rom som det fundamentale, og legger merke til at det i kvantemekanikken er prinsipielt umulig å kjenne en partikkels bane i detalj. Dermed sier Feynman at vi for å beregne sannsynligheten for at en partikkel skal gå fra et sted til et annet må legge sammen sannsynlighetsamplituden for alle måtene dette kan skje på -- altså for alle mulige partikkelbaner. Sannsynligheten får en ved å ta absoluttkvadratet av denne summen. Videre er alle baner like sannsynlige, men de har forskjellig fase: Amplituden for hver bane er e^iS/$\hbar$, der S fås fra klassisk Lagrangeteori. Dette er situasjonen når partikkelen er alene i verden, beveger seg gjennom tomt rom og ikke har noen vekselvirkning. Den resulterende amplituden K(1,2) for å gå fra punkt 1 til punkt 2, som kalles propagatoren, vil hovedsakelig bestå av bidragene fra baner som ligger nær den klassiske, og kan regnes som et `primitivt' element i teorien.

Dersom vi har å gjøre med to identiske partikler, som fremdeles ikke vekselvirker, må vi ta hensyn til at vi ikke kan vite vilken av de to vi observerer når hver av dem har gått fra et punkt til et annet. Vi har altså to muligheter (linjene representerer nå integralet av alle mulige baner fra det ene punktet til det andre):

For bosoner må vi legge sammen amplitudene for disse to prosessene, mens vi for fermioner må trekke dem fra hverandre. På denne måten oppstår effekten at bosoner liker hverandre, mens fermioner avskyr hverandre. For eksempel ser vi at sannsynligheten for at to fermioner med samme spinn ender i samme punkt er lik null, mens den for bosoner er større enn man `skulle vente'.

Når det er vekselvirkninger i systemet, må en også regne med alle de mulige måtene vekselvirkningen kan foregå på. I relativistisk teori i Feynman-bildet skjer all vekselvirkning ved emisjon og absorpsjon (skapelse og ødeleggelse) av bosoner som formidler vekselvirkningen.¹ Disse emisjonene og absorpsjonene kan foregå hvor som helst i tid og rom og i en vilken som helst orden, og en må altså summere opp amplitudene for alle disse mulighetene. Resultatet blir nøyaktig det samme som ved potensrekkeutviklingen av S-matrisen, og den diagrammatiske fremstillingen av prosessene er fra Feynmans side naturligvis ment å forestille partiklenes bevegelse i tid og rom.

For ladete partikler må en dessuten regne med ikke bare baner hvor partikkelen går fremover i tid, men også at de kan gå bakover i tid. Slike baner kan observeres som antipartikler.

Dette er veldefinert og helt i orden matematisk,² og har klare fordeler, ved at en slipper å behandle hver for seg en del prosesser som er umulige å skille eksperimentelt, og som bare skiller seg fra hverandre i den rekkefølgen i tid romlig atskilte emisjoner eller absorpsjoner skjer -- et begrep som heller ikke er relativistisk invariant. Dette kan illustreres ved to eksempler, som angitt i figuren nedenfor.

I det første eksemplet behøver en ikke å behandle tilfelle a) og b) separat, dvs. en behøver ikke å bekymre seg for vilket elektron som emitterer det virtuelle fotonet og vilket som absorberer det. Formalismen gjør ingen forskjell på emisjon og absorpsjon, og en kan like gjerne si at det i tilfelle b) er elektron 1 som emitterer et foton som går bakover i tid og absorberes av elektron 2 (en kan ikke se forskjell på et foton som går fremover og et som går bakover i tid -- fotonet er sin egen antipartikkel). Ved en passende Lorentz-transformasjon kan da også diagram b) bringes over i formen a) (virtuelle fotoner behøver ikke å bevege seg med lyshastigheten) -- de to kan og skal altså behandles under ett.³

I eksempel 2 kan diagram b) og c) behandles under ett, mens diagram a) må behandles separat. Vi ser altså at det ikke er rekkefølgen i tid av emisjon og absorpsjon, men snarere rekkefølgen langs elektronets verdenslinje som er av avgjørende betydning. Diagram c) kan tolkes (tradisjonelt) som at det ene fotonet skaper et elektron-positron-par ved B, hvorpå positronet går til A og annihilerer elektronet der -- eller (Feynman) som at elektronet går til A, emitterer et foton, snur og løper tilbake i tid for å absorbere fotonet ved B, for så å snu igjen og oppføre seg `skikkelig'.⁴