Quantum vs Classical Computation
Quantum Computing is the art of using all the possibilities that the laws of quantum mechanics give us to solve computational problems. Conventional, or "Classical" computers (like the one used to build this page) only use a small subset of these possibilities. In essence, they compute in the same way that people compute by hand. There are many results about the wonderful things we would be able to do if only we had a large enough quantum computer. The most important of these is probably that we would be able to perform simulations of quantum mechanical processes in physics, chemistry and biology, which will never come within the range of classical computers. Let's compare some aspects of classical and quantum computers.
Classical Computing
Quantum Computing
Information is stored in bits, which take the discrete values 0 and 1.
If storing one number takes 64 bits, then storing N numbers takes N times 64 bits.
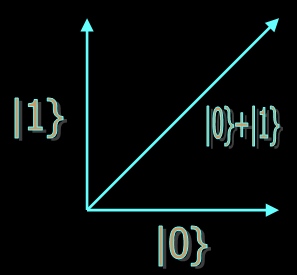
Information is stored in quantum bits, or qbits. A qbit can be in states labelled |0} and |1}, but it can also be in a superposition of these states, a|0} + b|1}, where a and b are complex numbers. If we think of the state of a qbit as a vector, then superposition of states is just vector addition.
For every extra qbit you get, you can store twice as many numbers. For example, with 3 qbits, you get coefficients for |000}, |001}, |010}, |011}, |100}, |101}, |110} and |111}.
Calculations are done essentially in the same way as by hand. As a result, the class of problems that can be solved efficiently is the same as the class that can be solved efficiently by hand. Here "efficiently", refers to the idea that the evaluation time doesn't grow too quickly with the size of the input.
Calculations are performed by unitary transformations on the state of the qbits. Combined with the principle of superposition, this creates possibilities that are not available for hand calculations (see the QNOT example on the right). This translates into more efficient algorithms for a.o. factoring, searching and simulation of quantum mechanical systems
The QNOT
The classical NOT-gate flips its input bit over;
NOT(1)=0, NOT(0)=1.
The quantum analogue, the QNOT also does this, but it flips all states in a superposition at the same time. So if we start with 3 qbits in the state
|000}+|001}+2|010}-|011}-|100}+3i|101}+7|110}
and apply QNOT to the first qbit,we get
|100}+|101}+2|110}-|111}-|000}+3i|001}+7|010}.