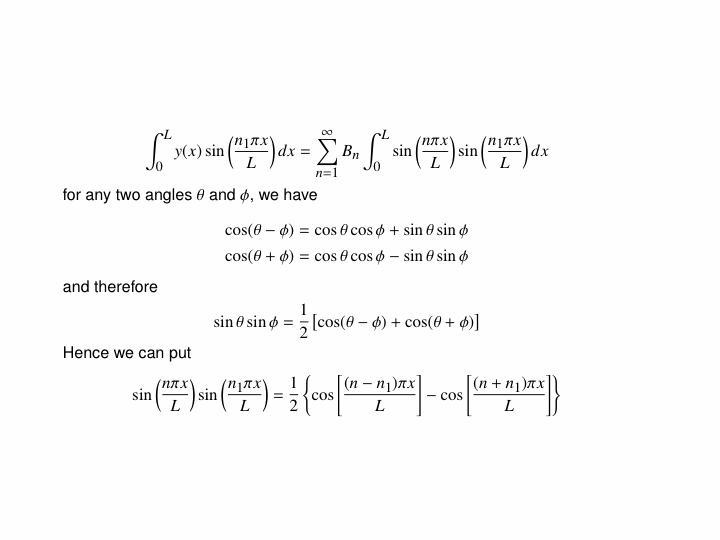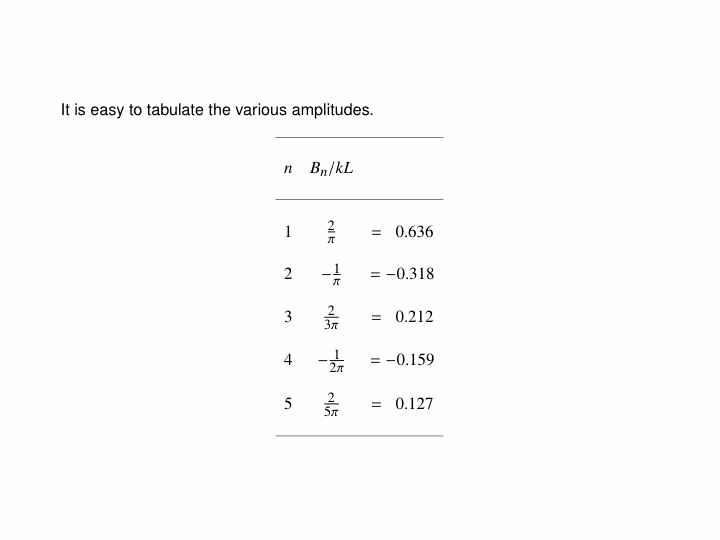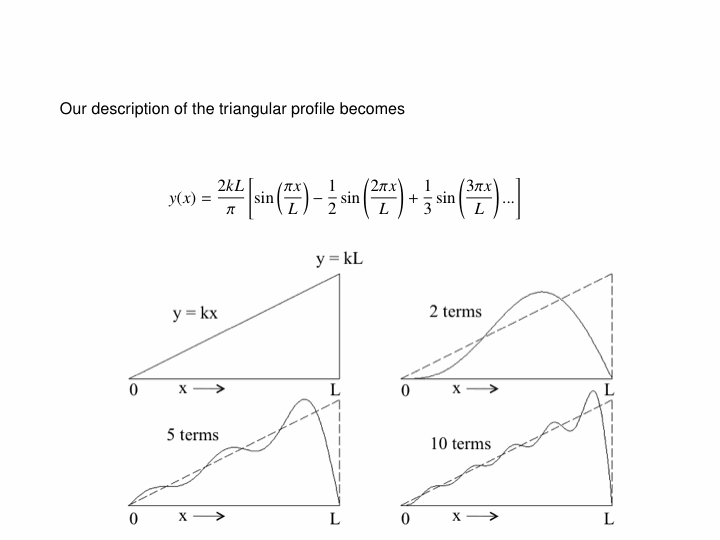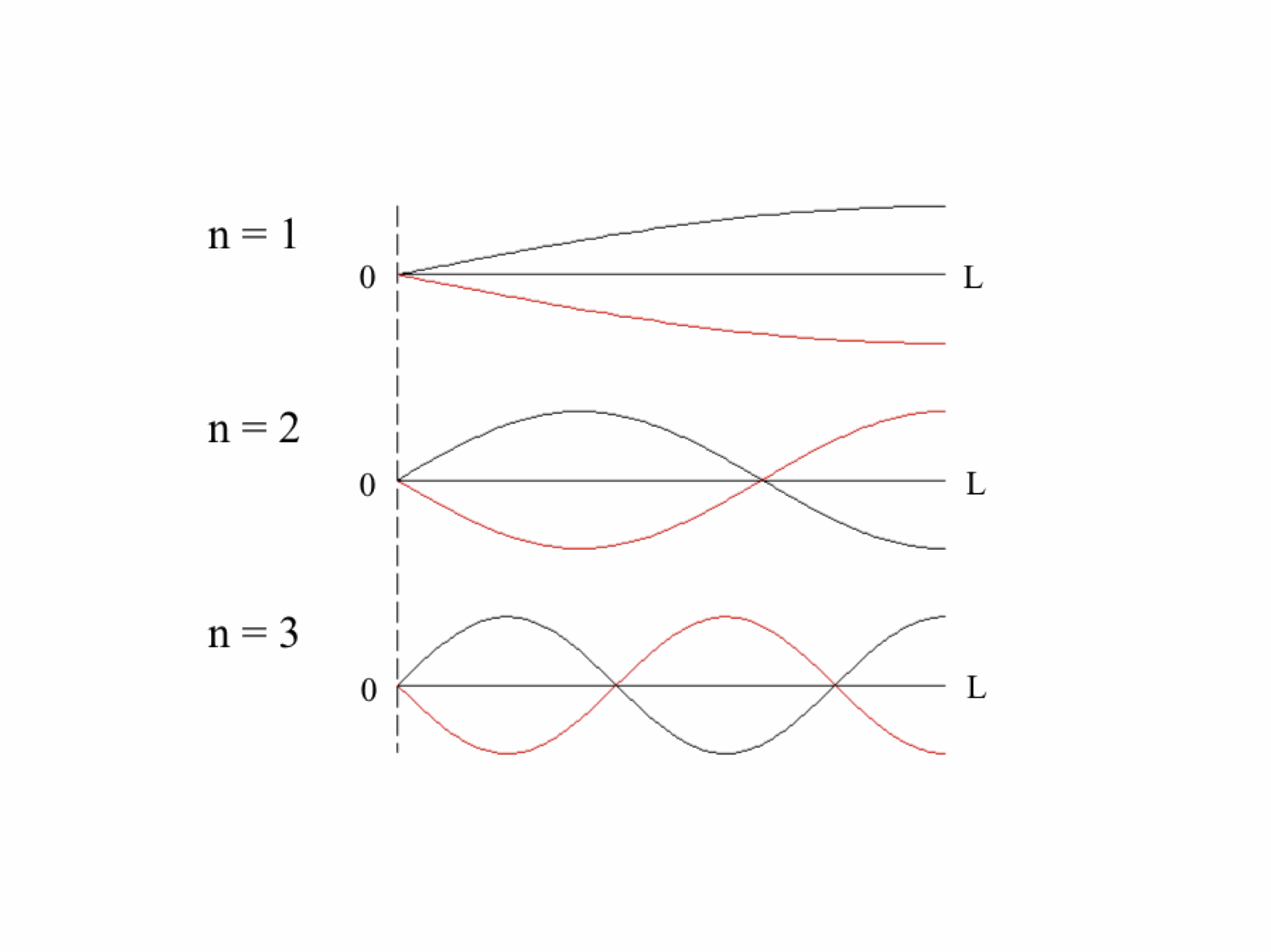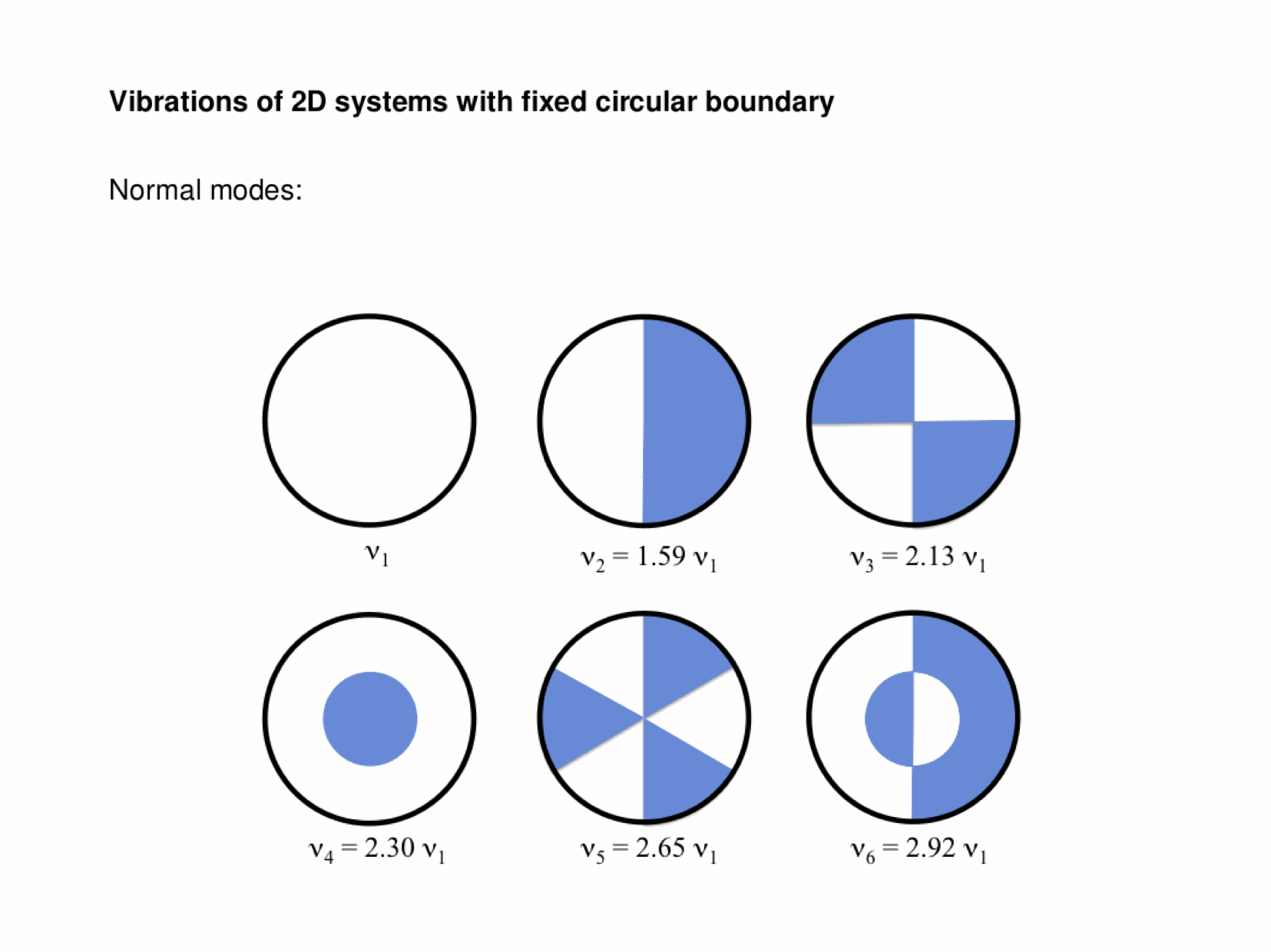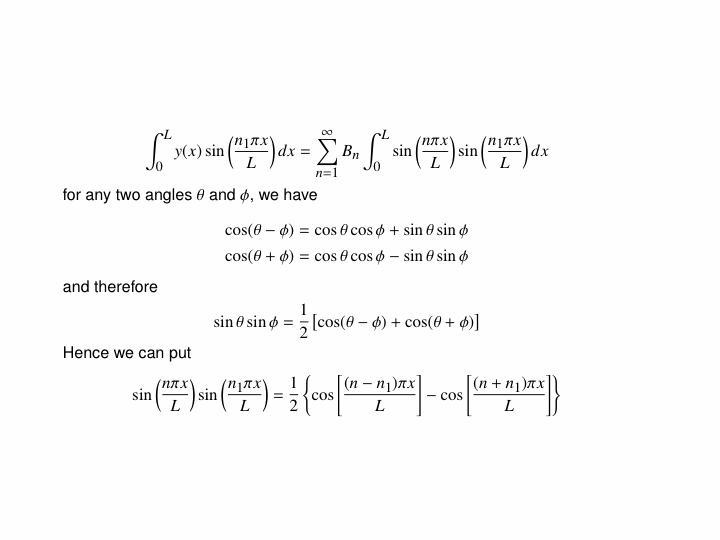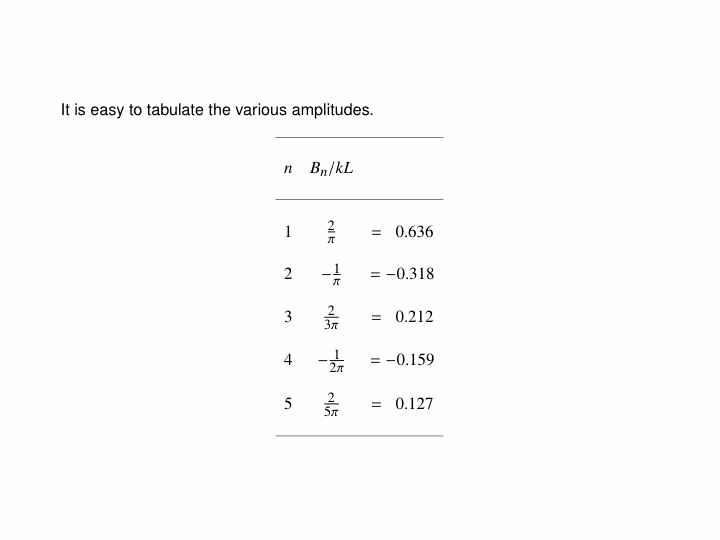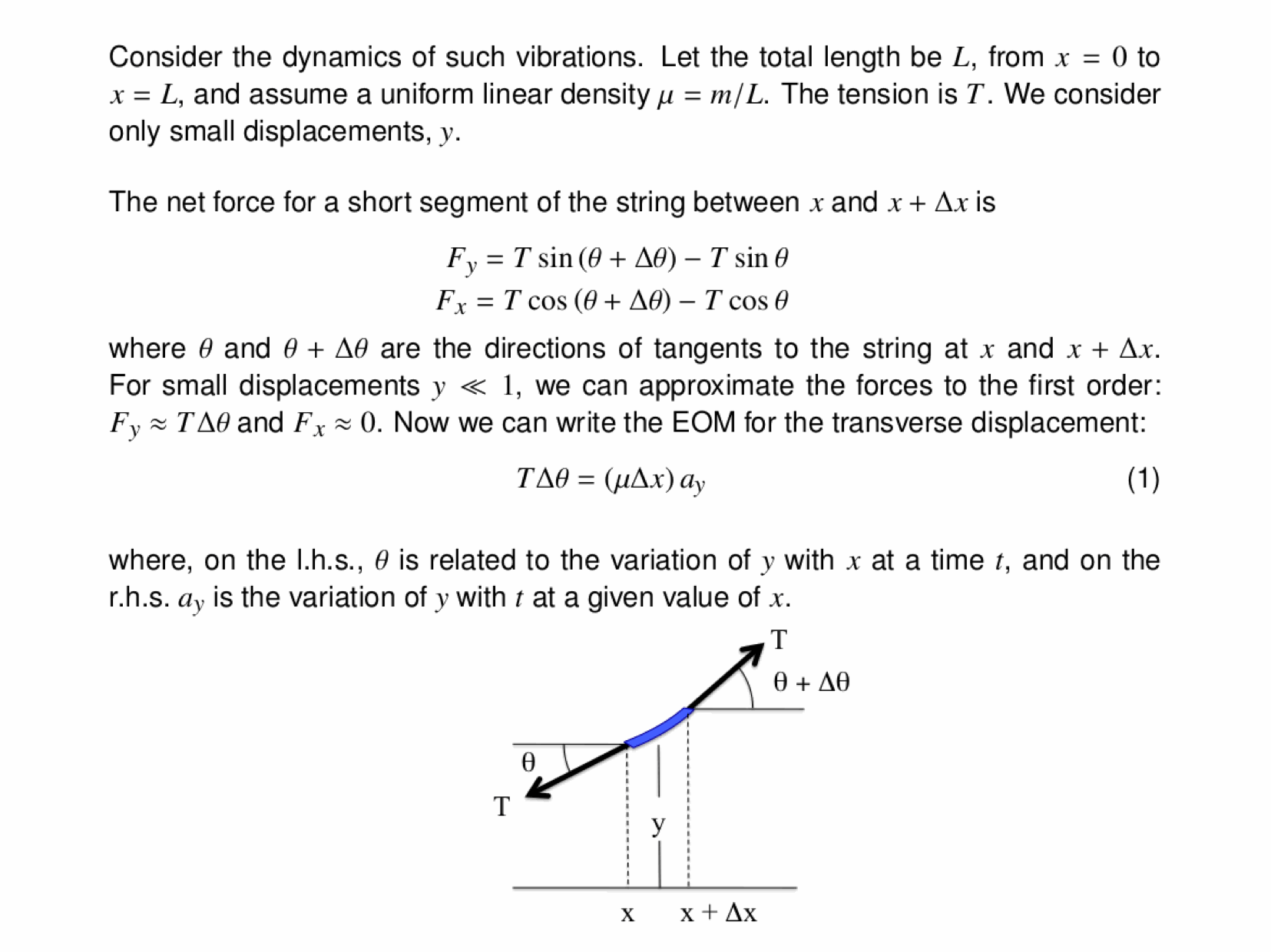
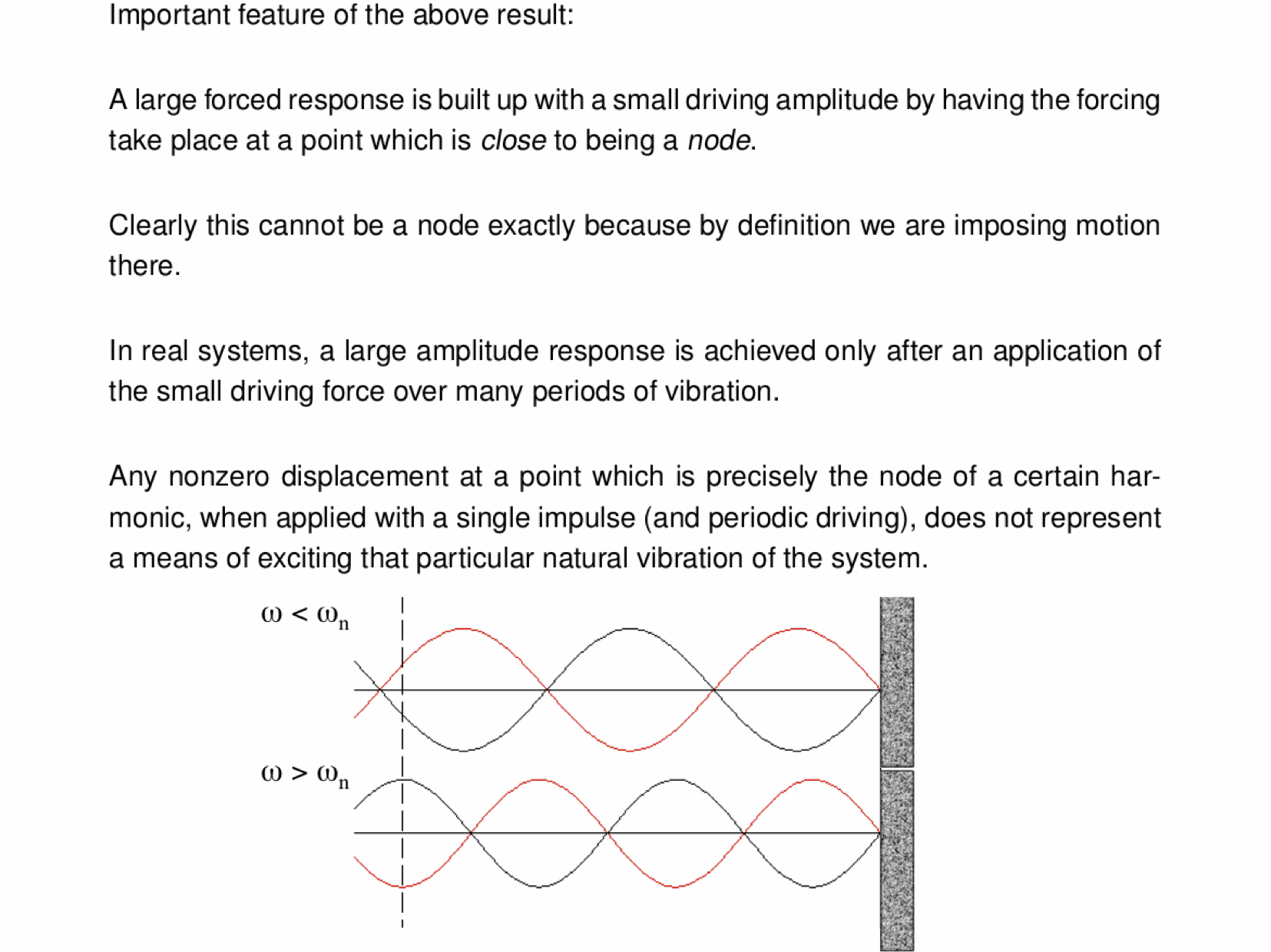
A quick comment on Fourier analysis...
Fourier series are very useful tools indeed, but they have their limits when applied to functions which are discontinuous. Consider a square wave of period 1 which, in the interval [0,1], is zero for $0\leq x\leq 1/4$ and $3/4\leq x\leq 1$
and 1 elsewhere. Below is an animation which shows the sequential addition of the first 100 nonzero terms in the Fourier expansion:
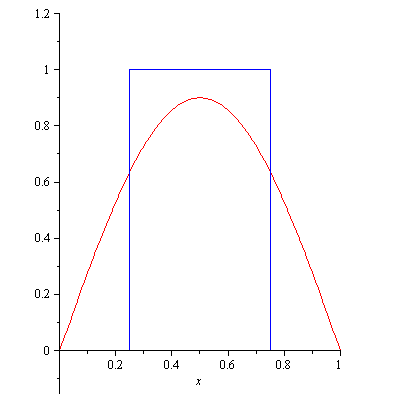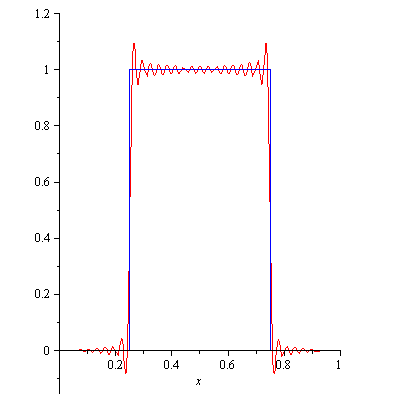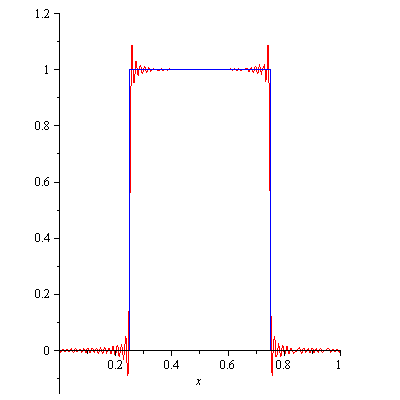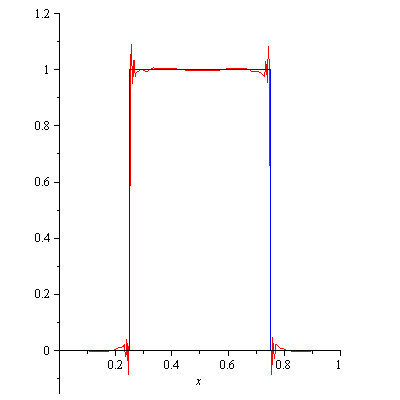
The sum gets closer and closer to the actual square wave everywhere except at the discontinuities $x=1/4$ and $x=3/4$, where there is always an over/undershoot. This is unavoidable, and persists no matter how many terms you include in the Fourier expansion. This is called the Gibbs phenomenon (after the American physicist Josiah Willard Gibbs).
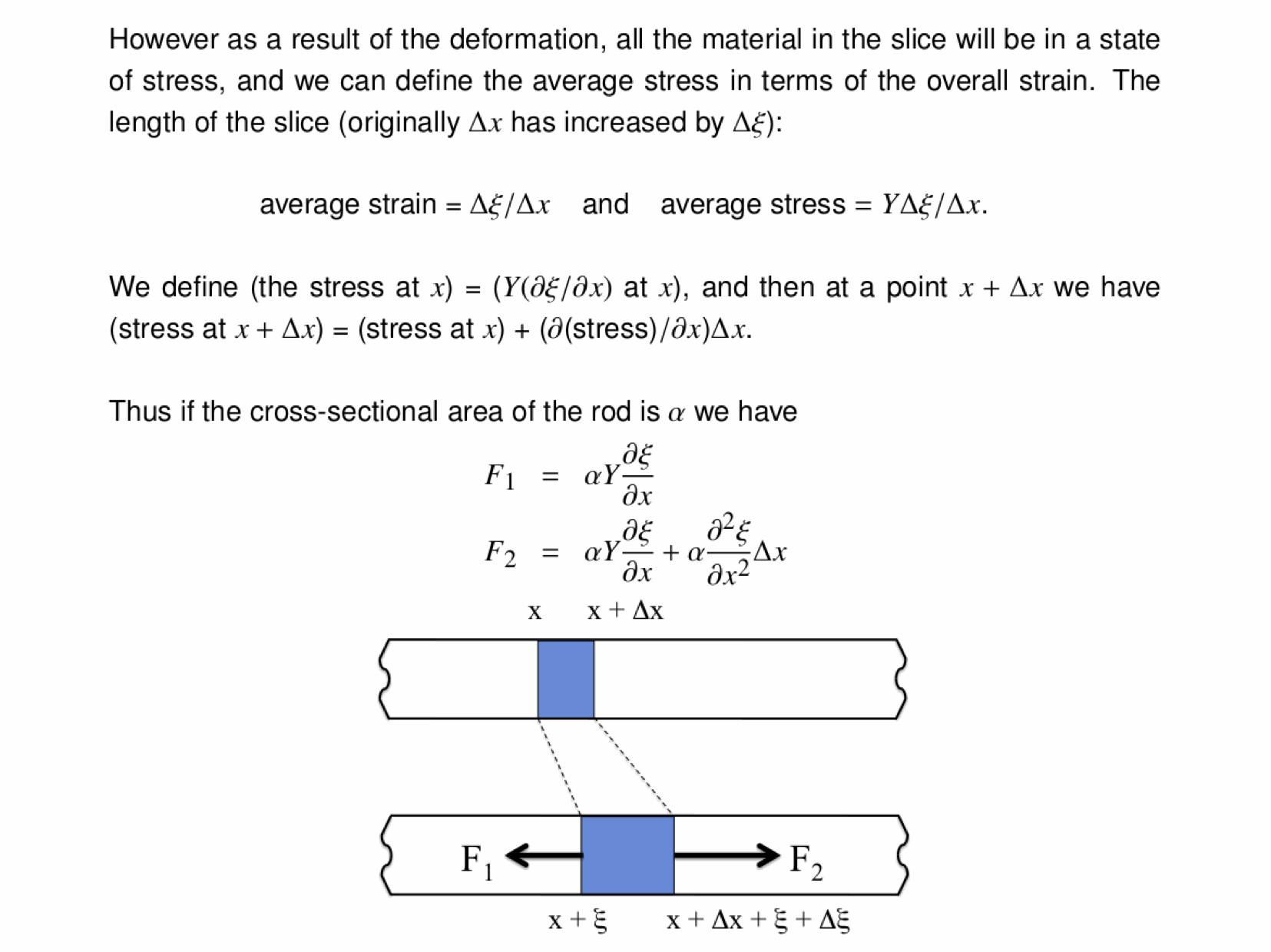
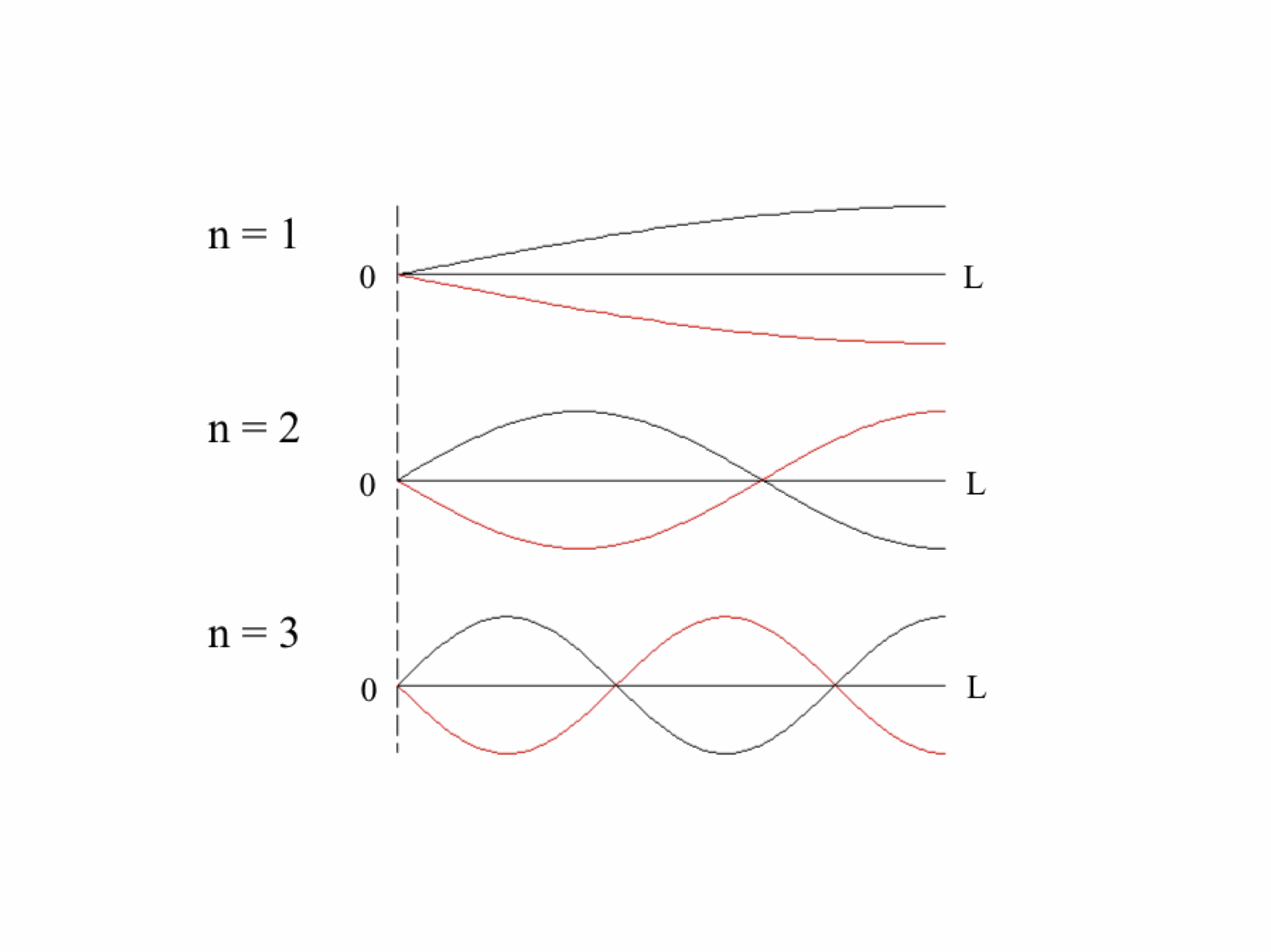
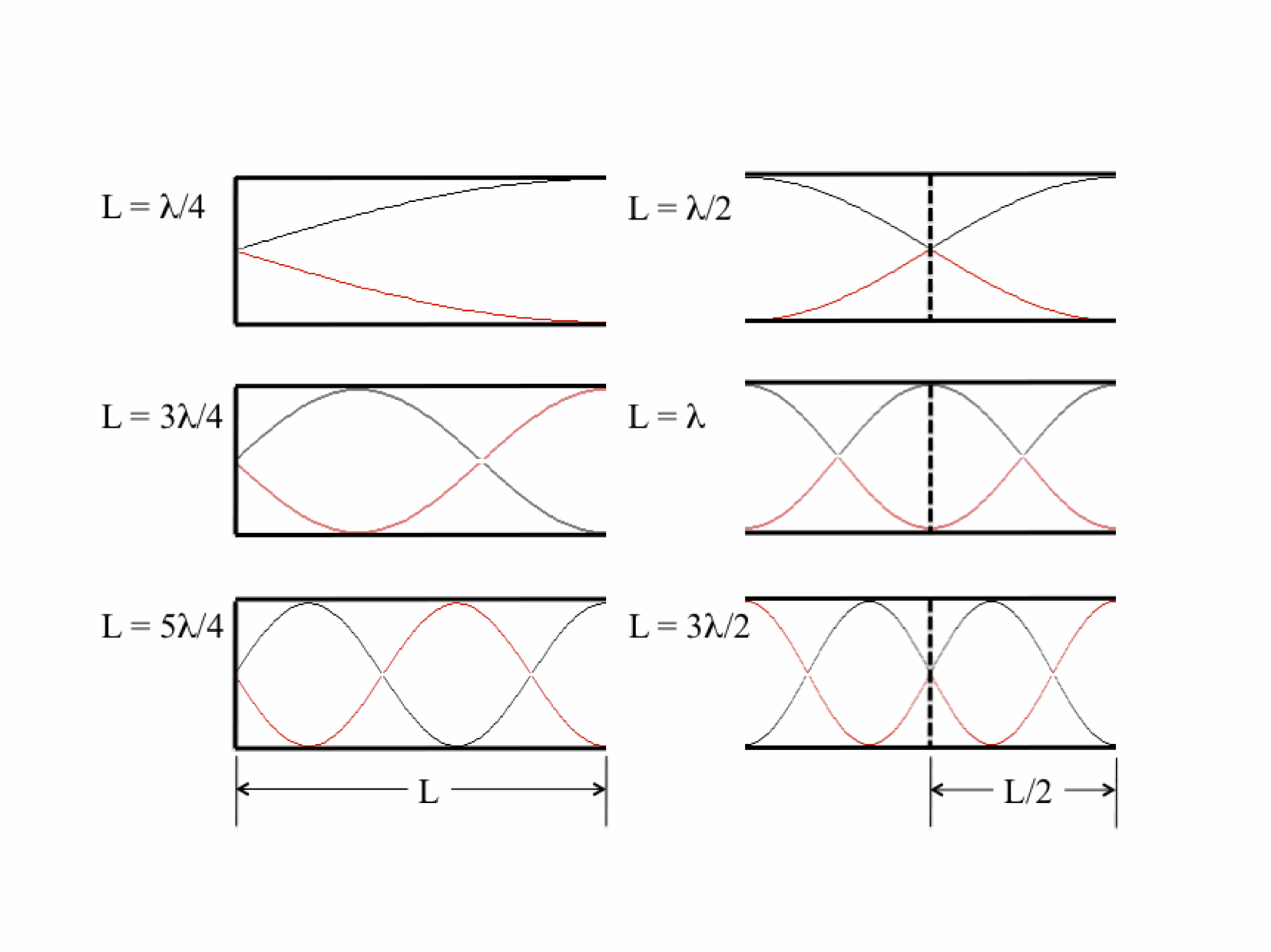
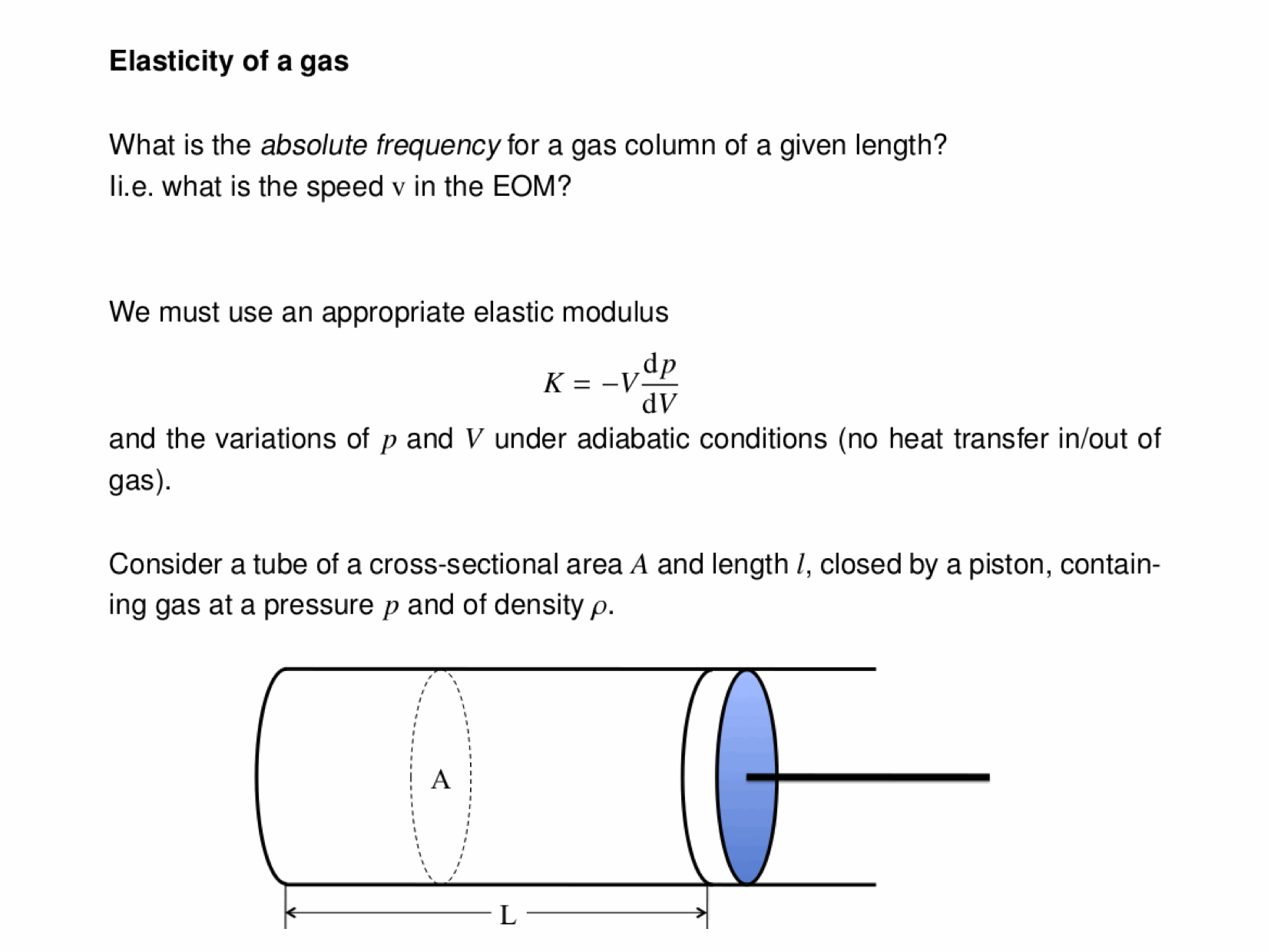
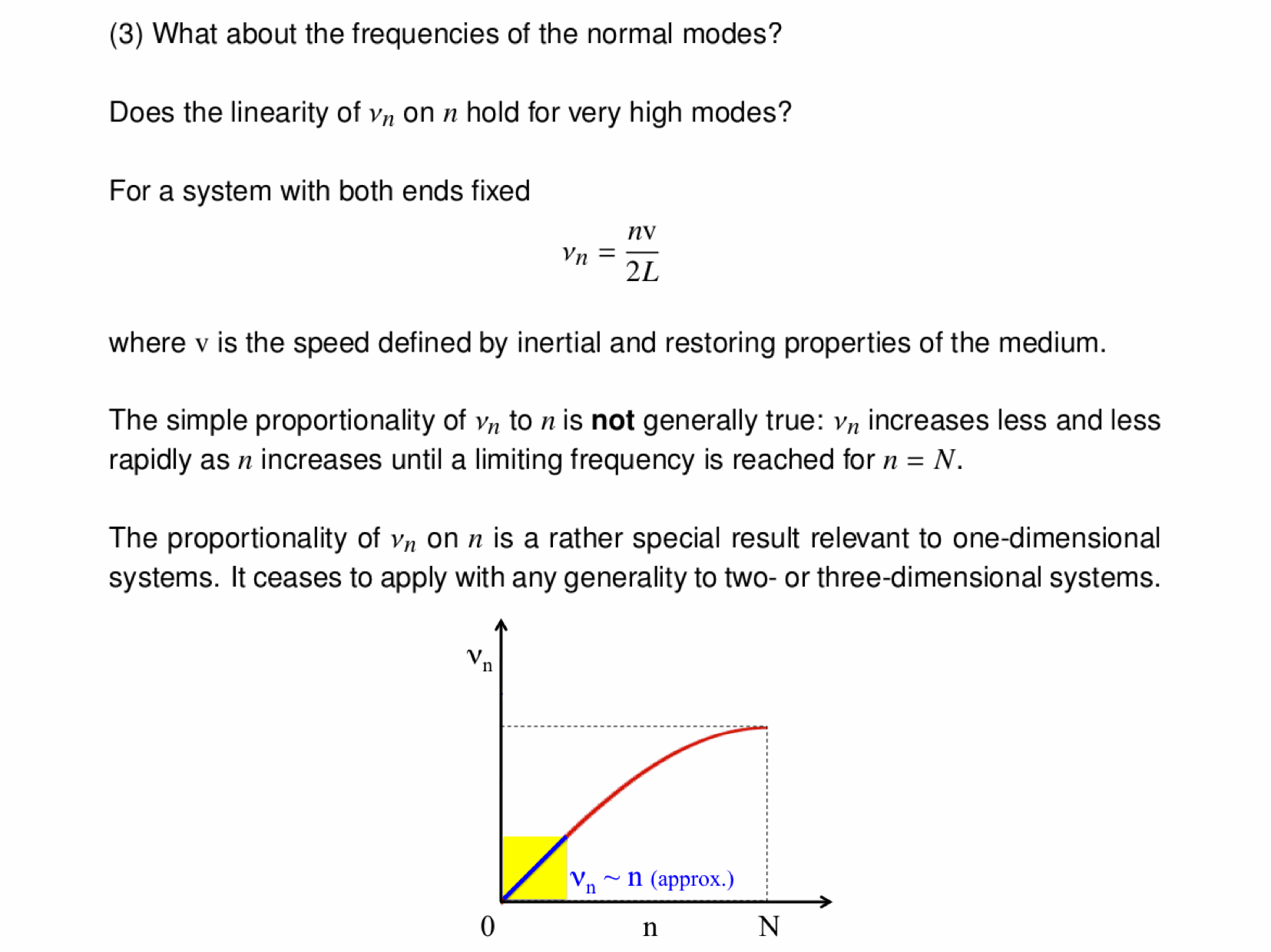
The normal modes of vibration of a column of gas -- say, the air within a tube -- depend on the boundary conditions, namely, whether or not the ends of the tube are open or sealed. The three animations below show the three lowest modes inside a tube with both ends closed, standing waves whose endpoints are fixed:
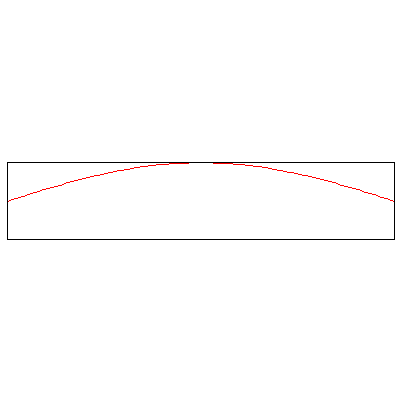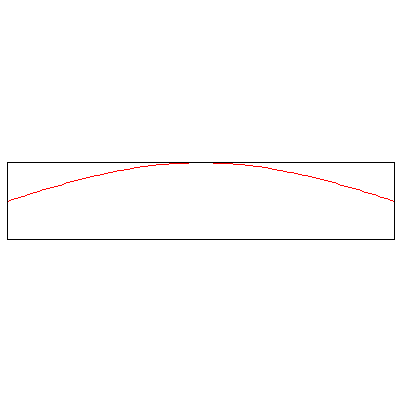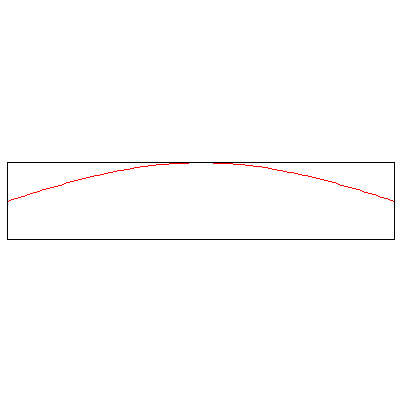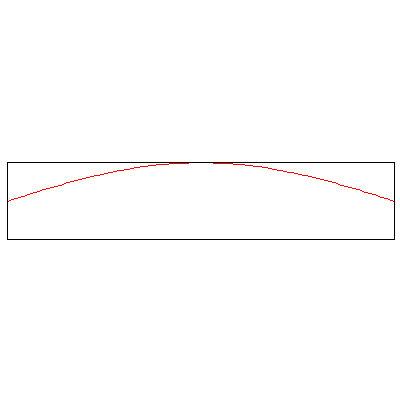
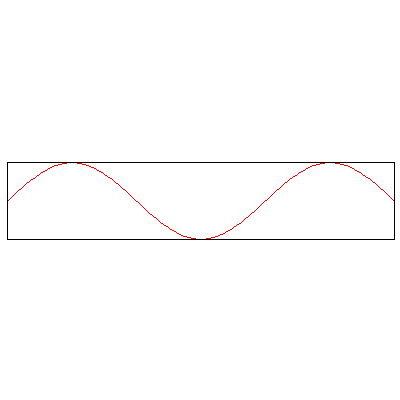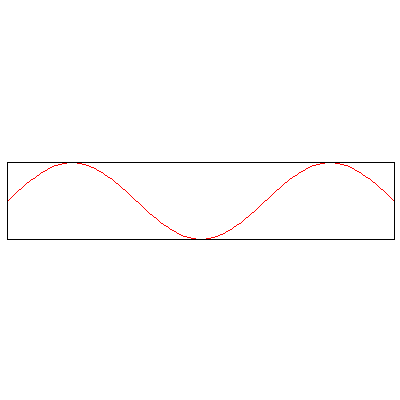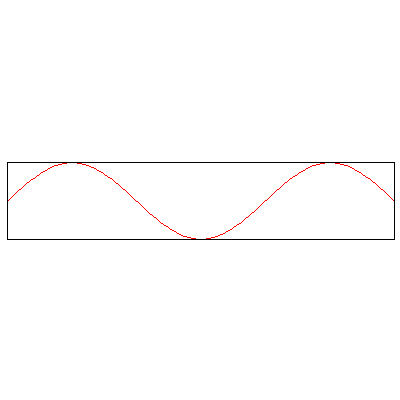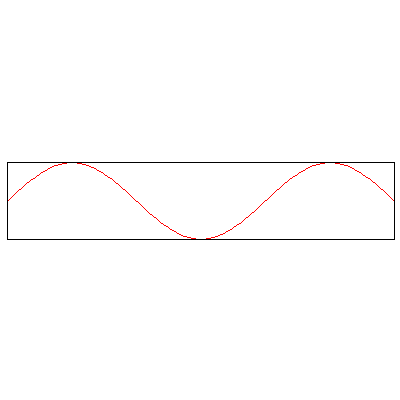Now, the three lowest modes when one end is open:
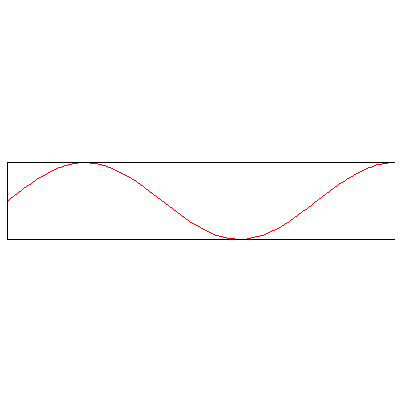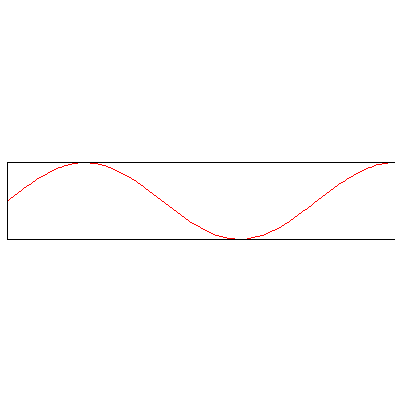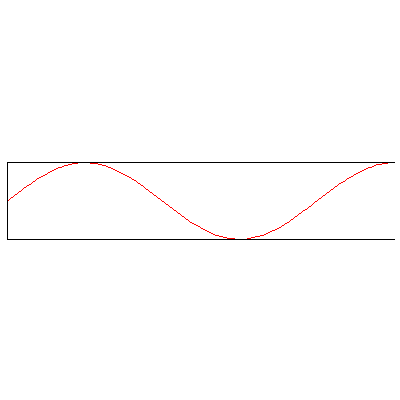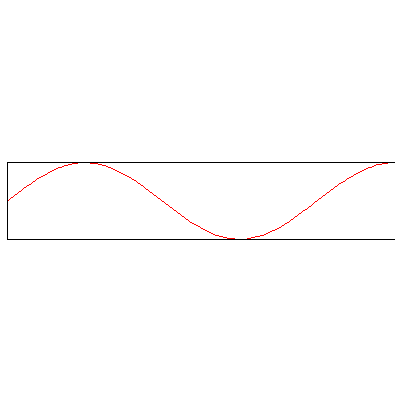And with both ends open:
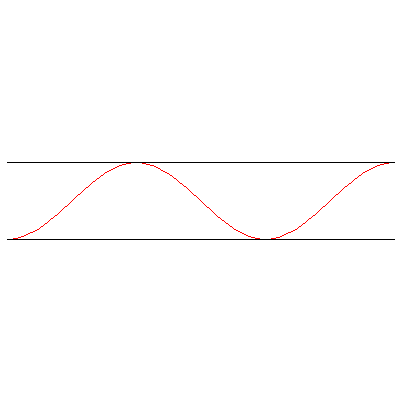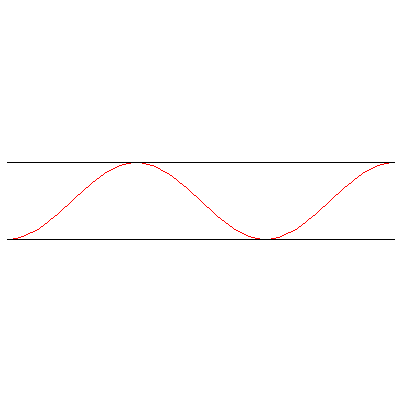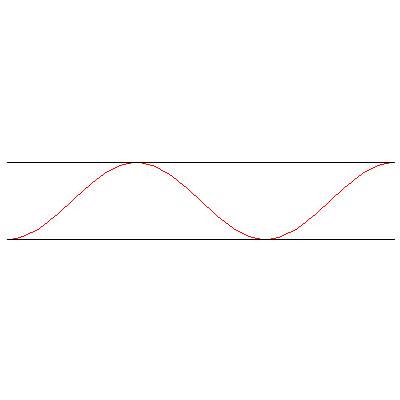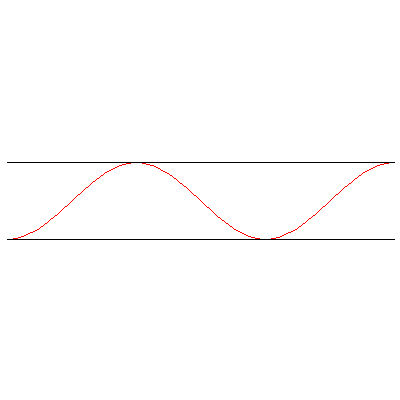(In all cases, the frequency is $\omega=12\pi/5\,\mathrm{rad}\cdot\mathrm{s}^{-1}$.)
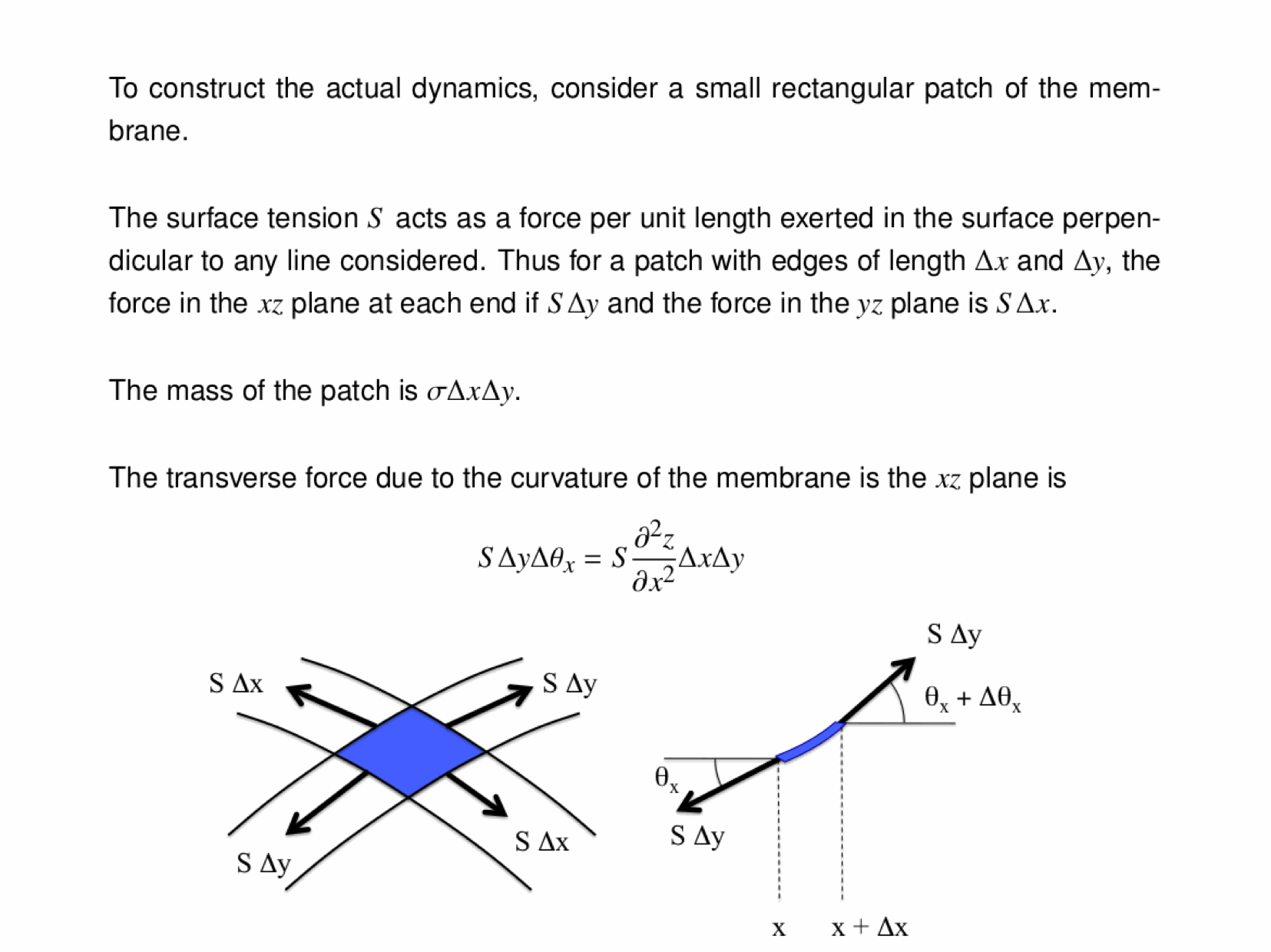
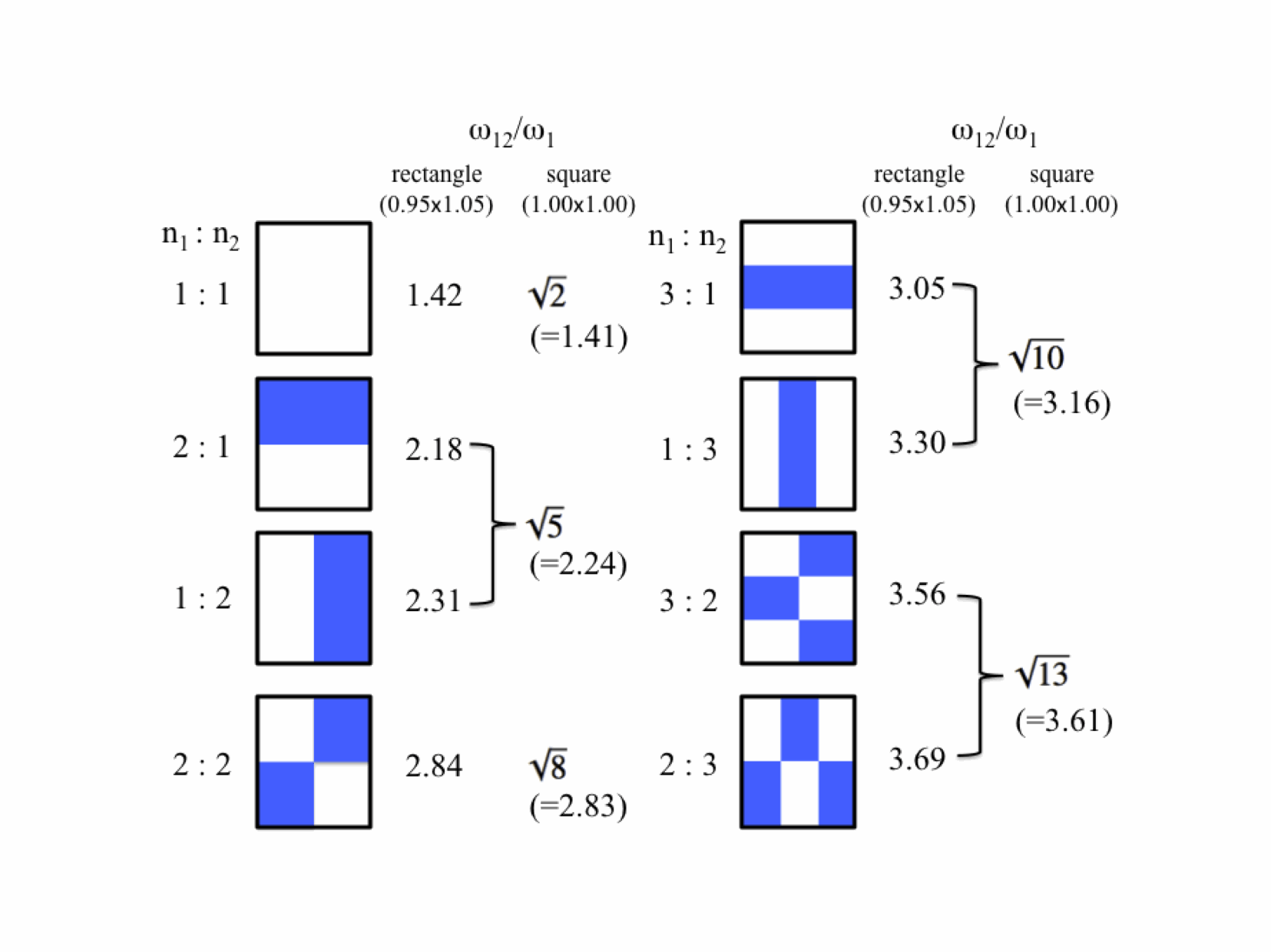
Normal modes exist for multidimensional systems as well. Below is an animation of a general vibration of a membrane stretched across a rectangular frame where one side is 1.5 times longer than the other:
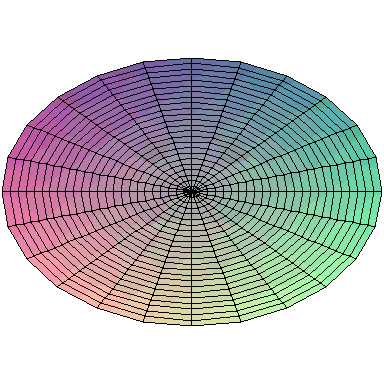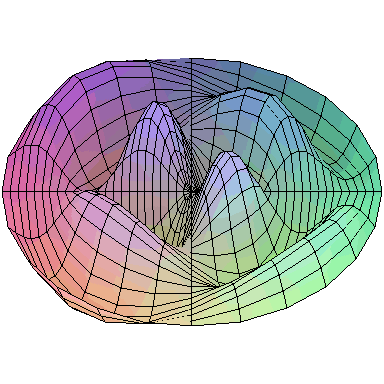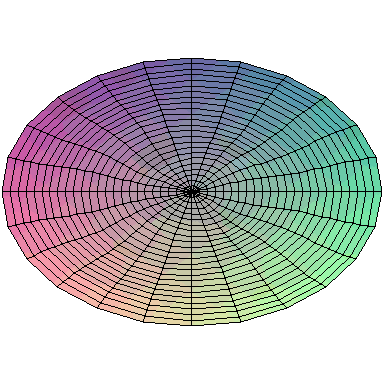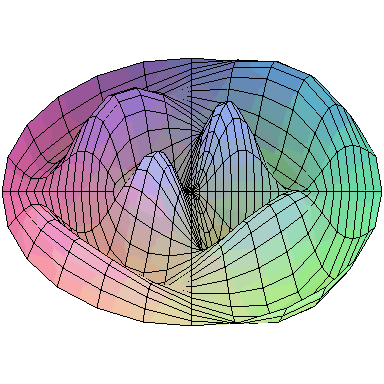
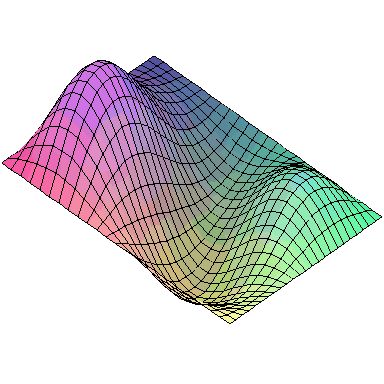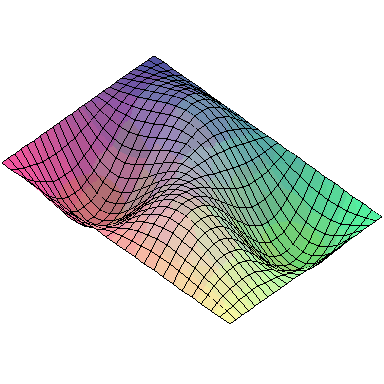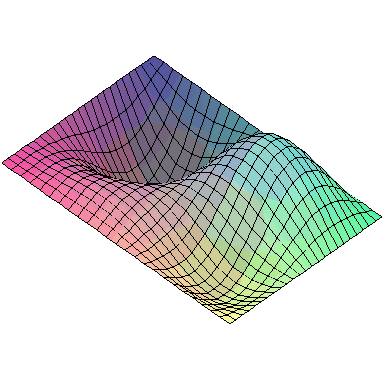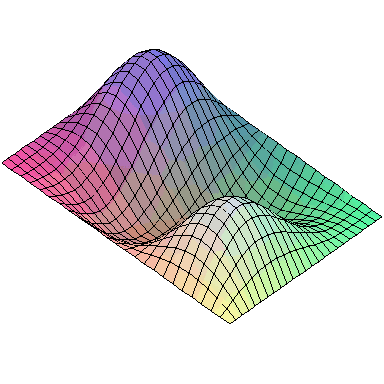And here are animations of the first nine normal modes:
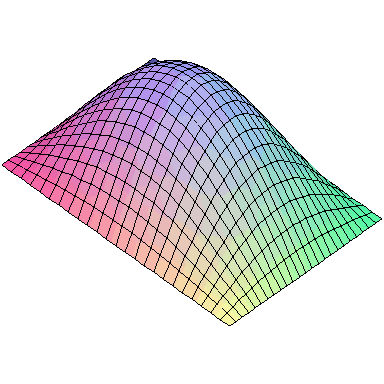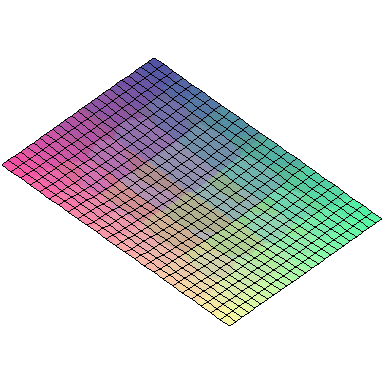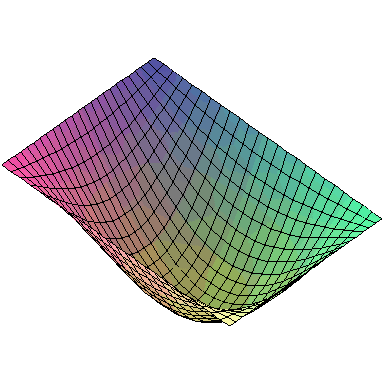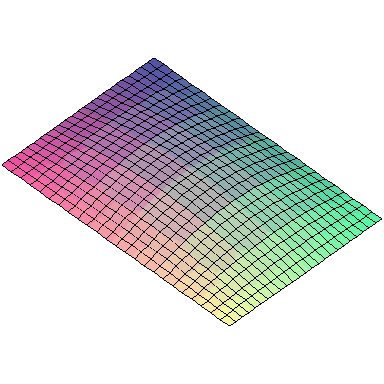
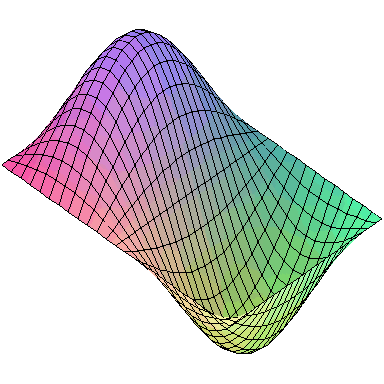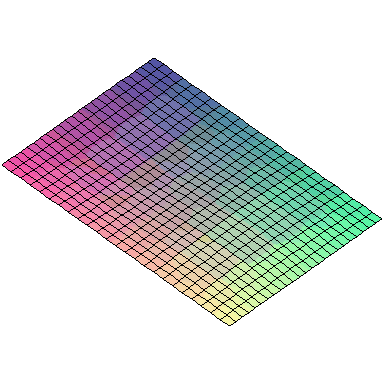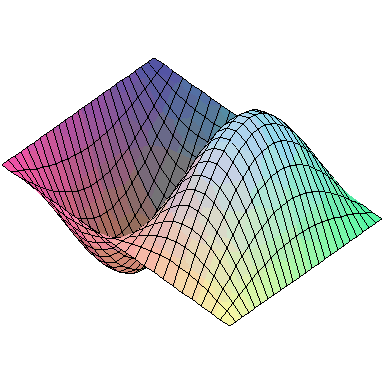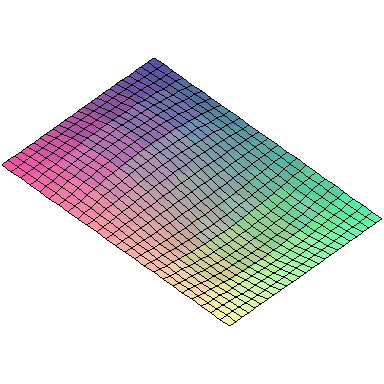
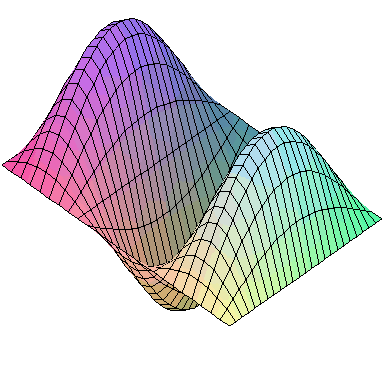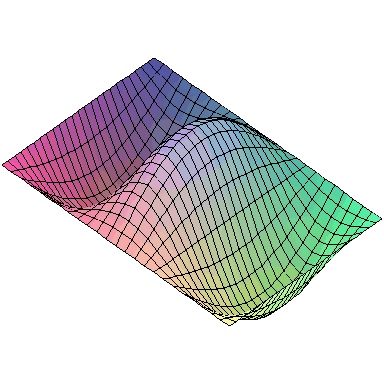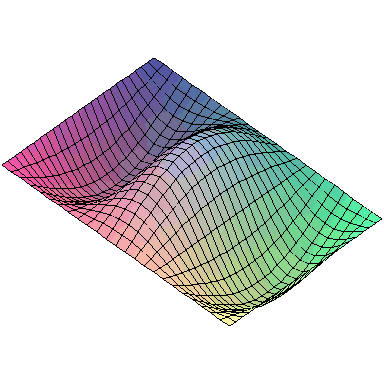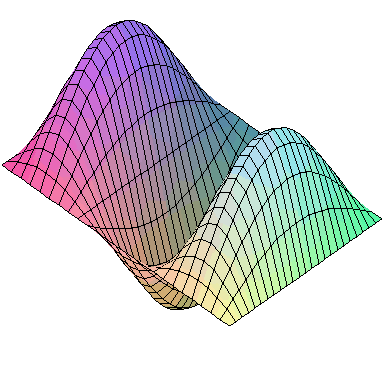
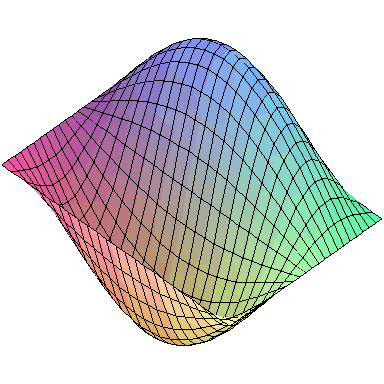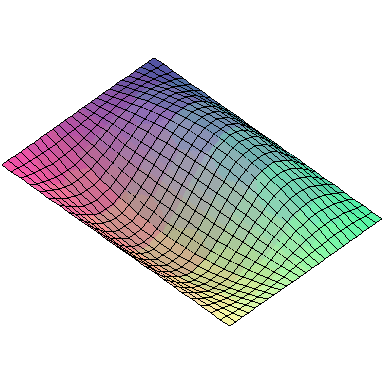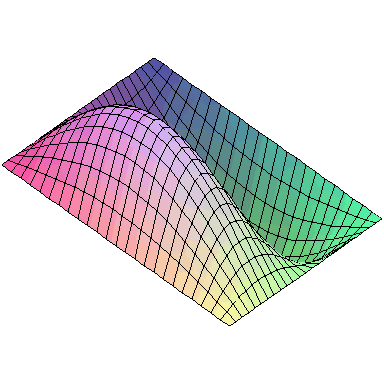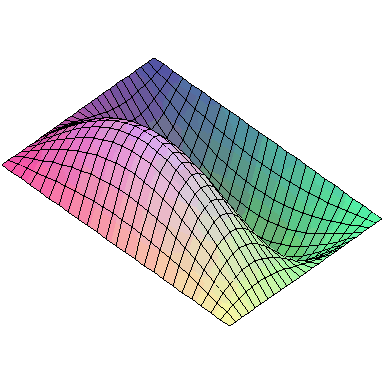
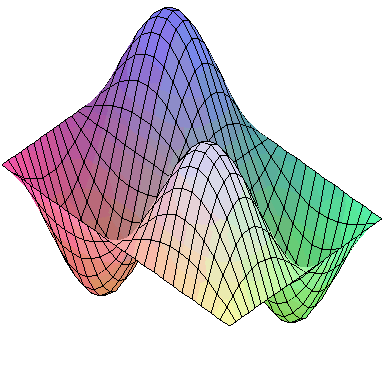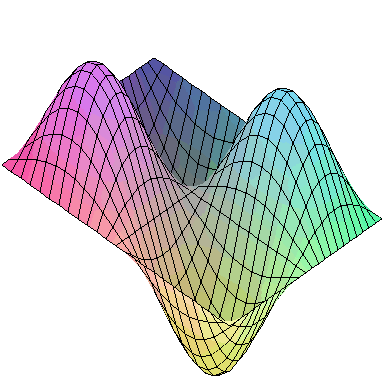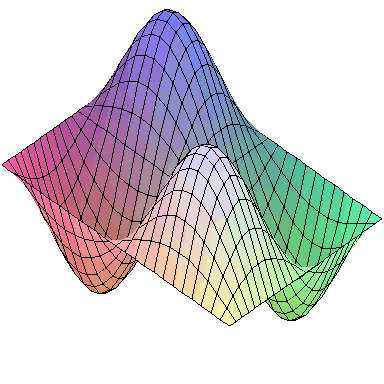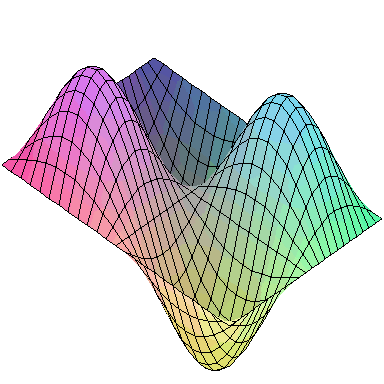
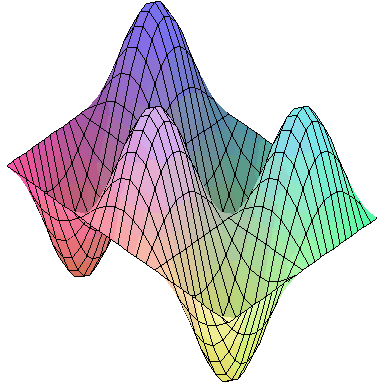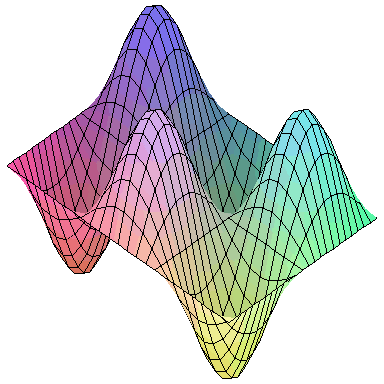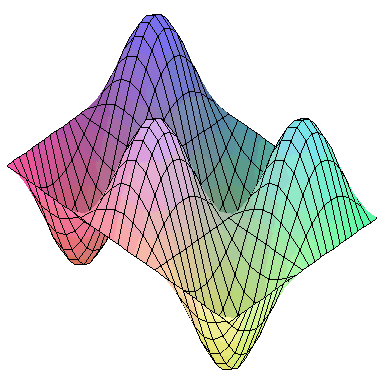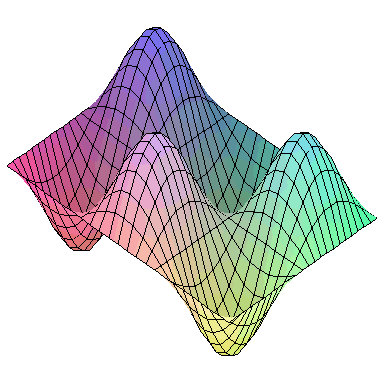
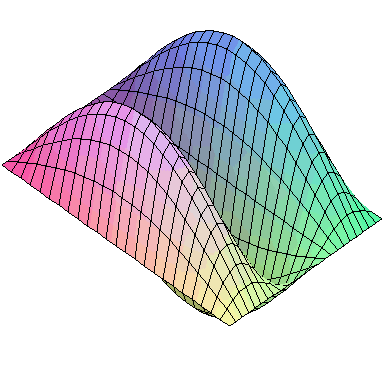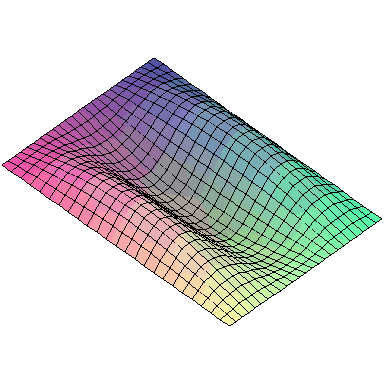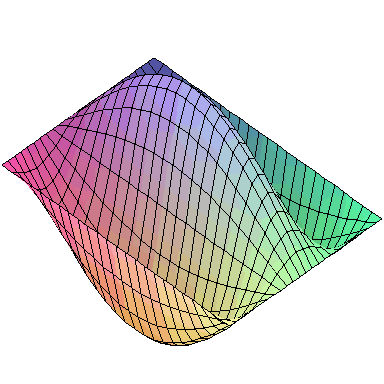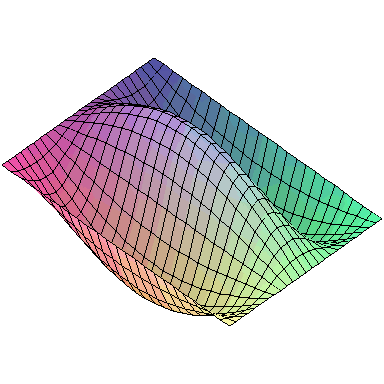
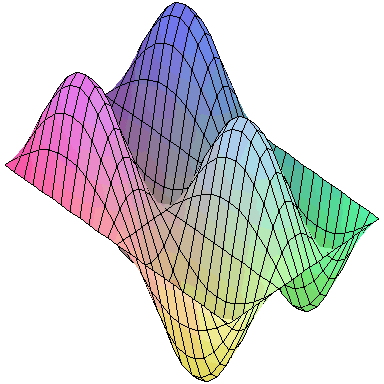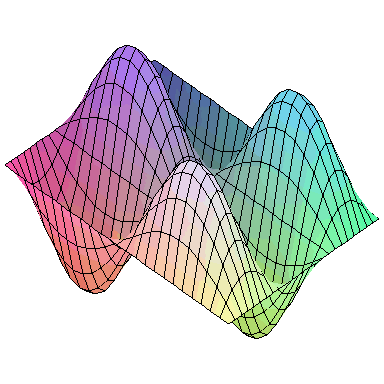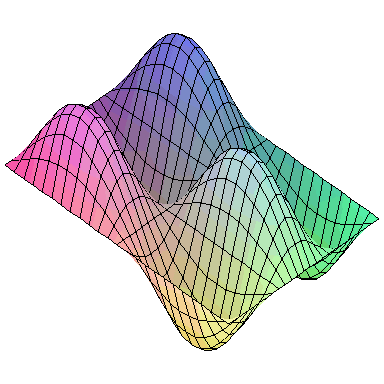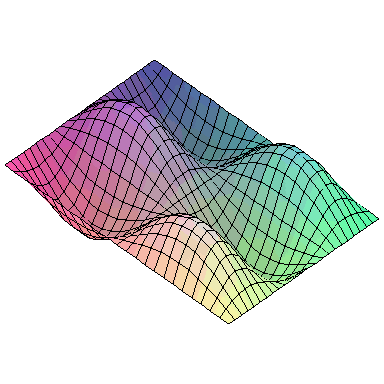
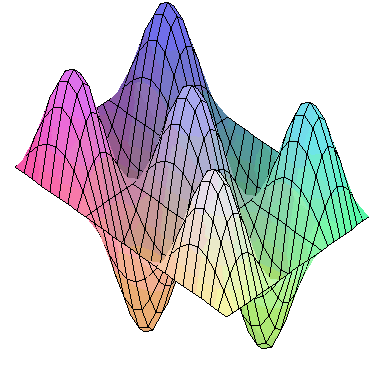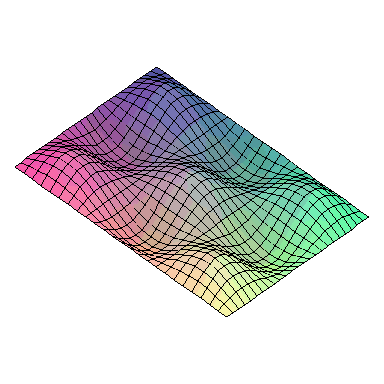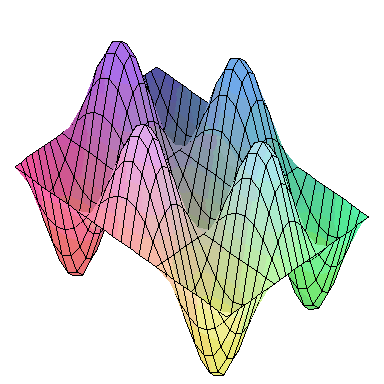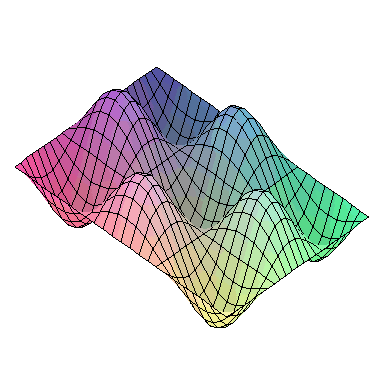
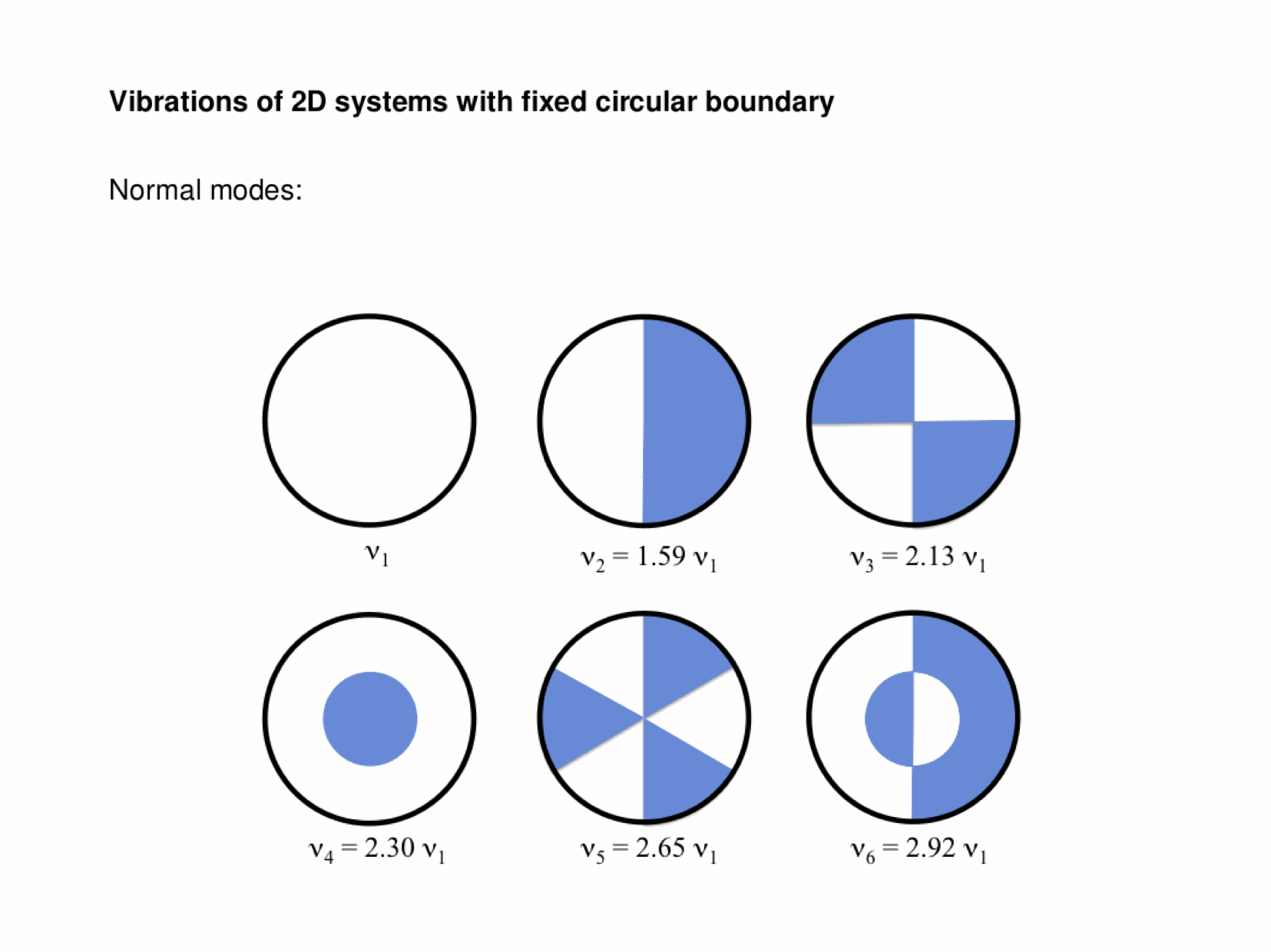
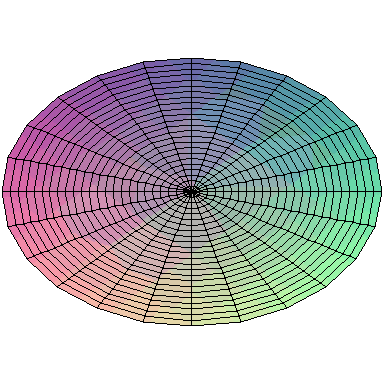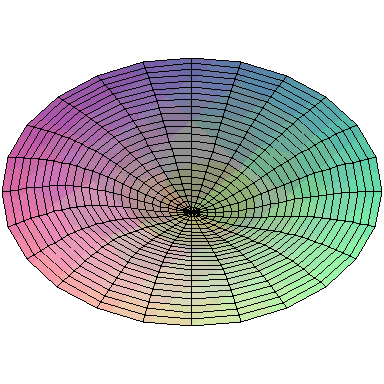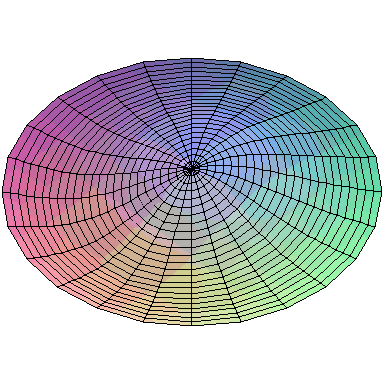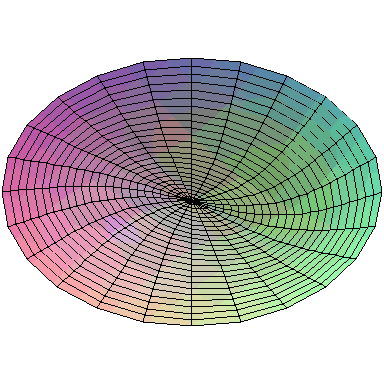
A general vibration might look like
and the first nine normal modes look like
