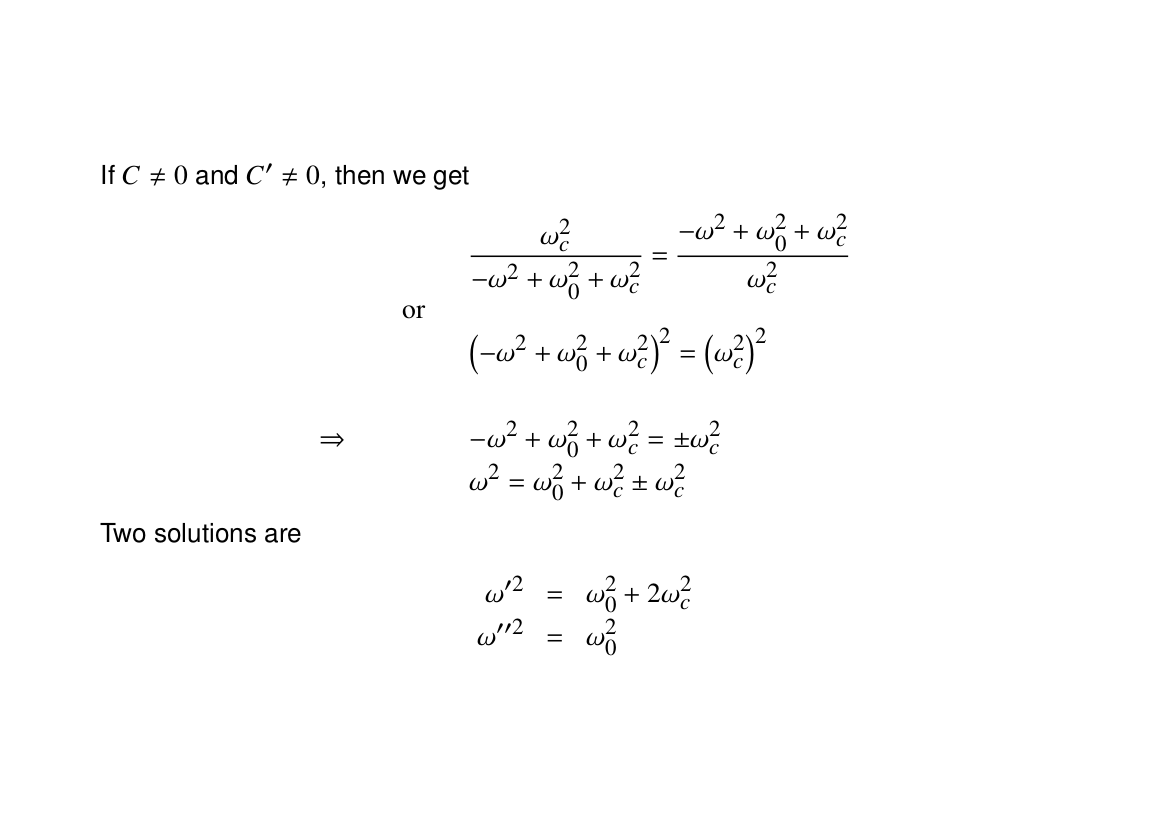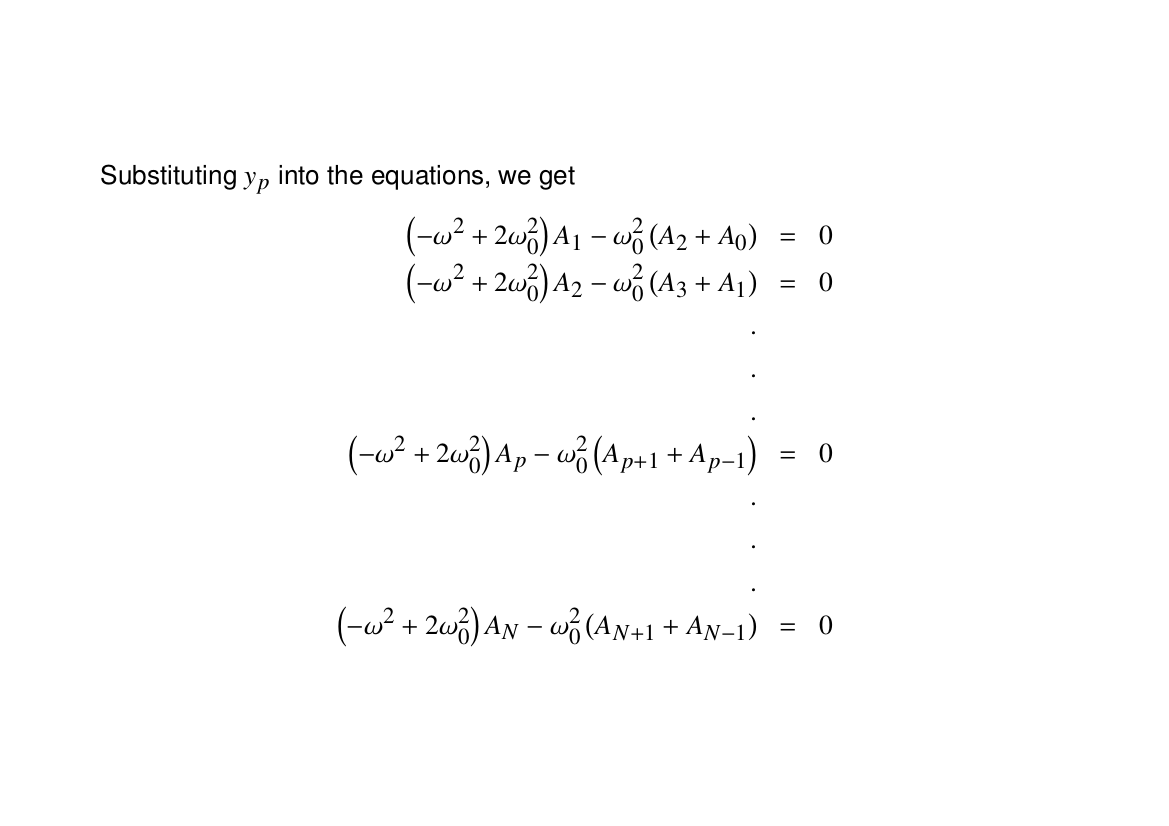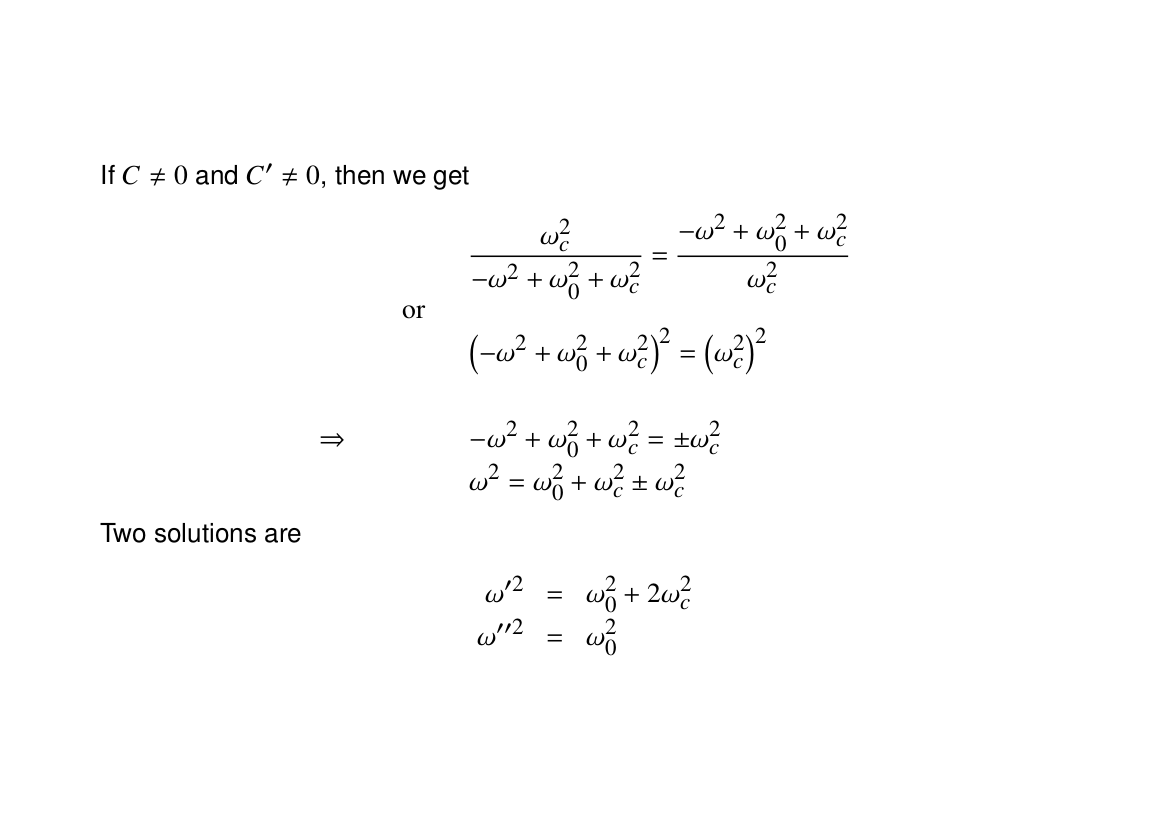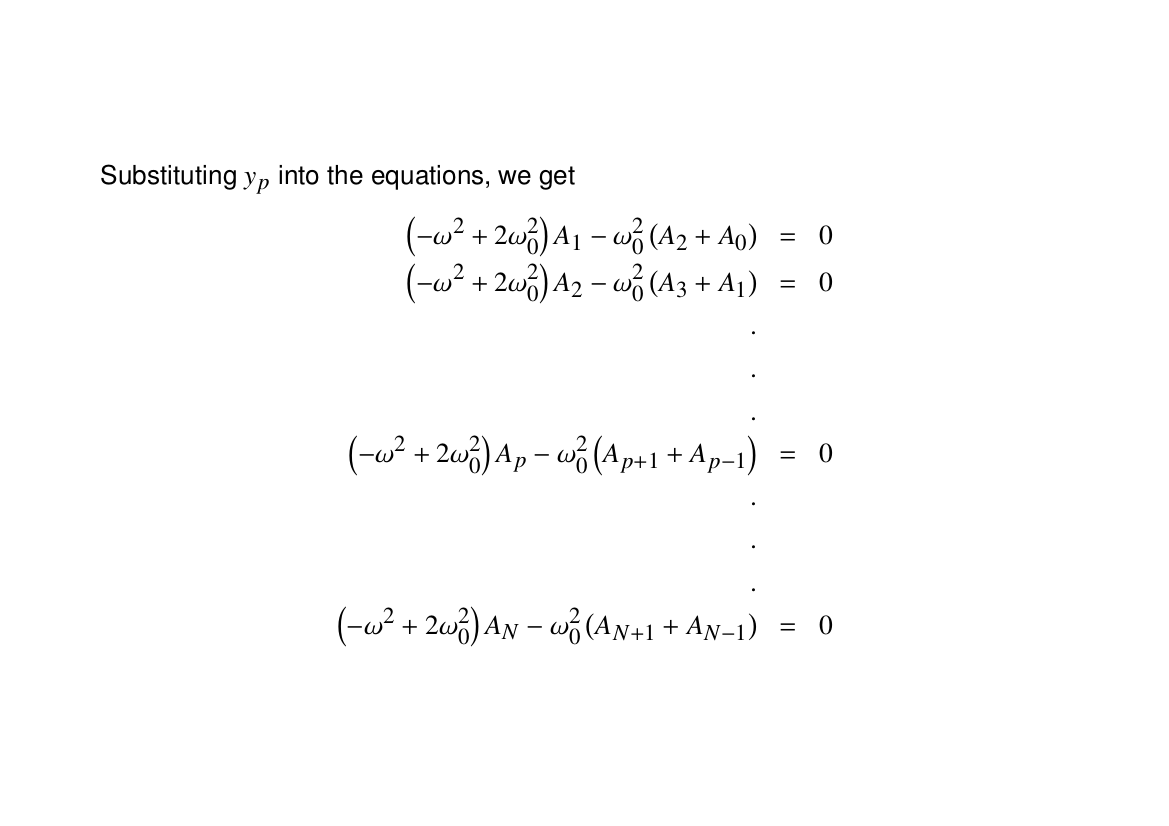
All of the animations below depict a variety of oscillations that two coupled pendula (initially at rest) can undergo. Although the masses of the two bobs may vary from case to case, the two lengths both correspond to 17.2 cm, i.e. a natural frequency of $\omega_0=12\pi/5\,\mathrm{rad}\cdot\mathrm{s}^{-1}$. We take the separation between the anchor points and the spring equilibrium length to always be 17.2 cm as well. (In order to make the animations clearer, the vertical motion of the bobs has been ignored.)

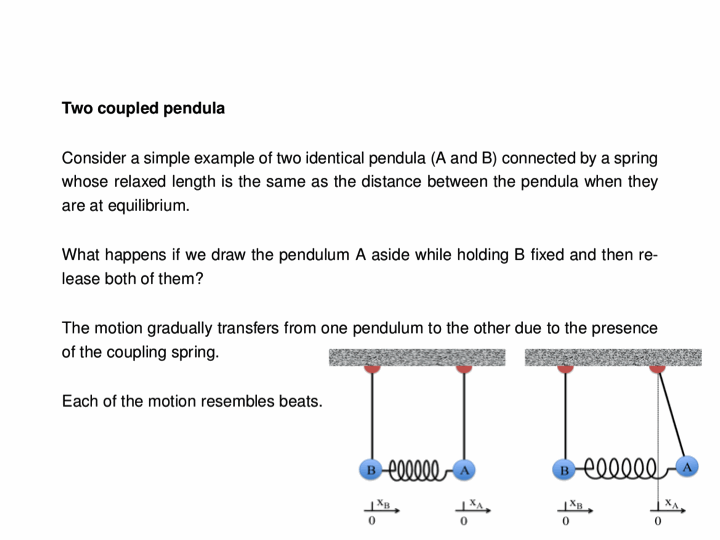
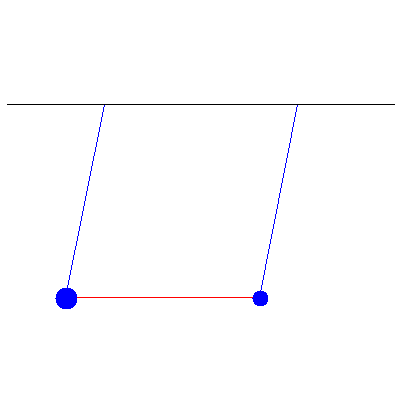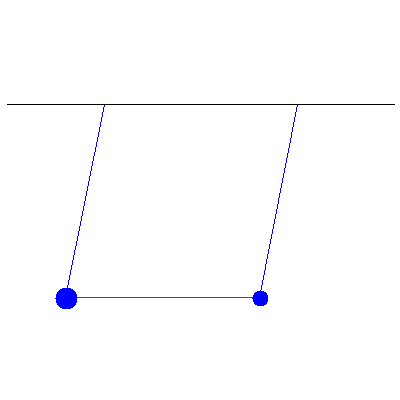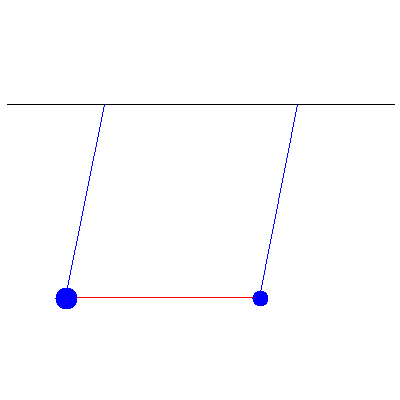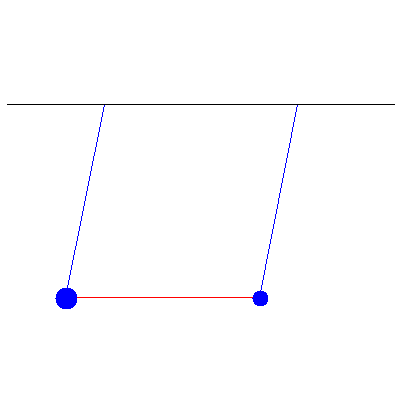
We first look at the simple case of two pendula of identical masses (100 g) connected by a spring of spring constant 0.57 $\mathrm{N}\cdot\mathrm{m}^{-1}$. One is initially pulled 5.2 cm to the left, while the other stays vertical. We then release both pendula and see an oscillation that "transfers" from one to the other, as shown below: 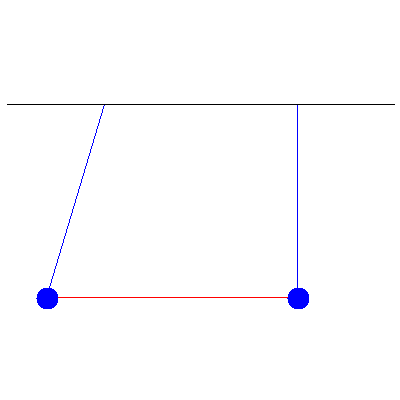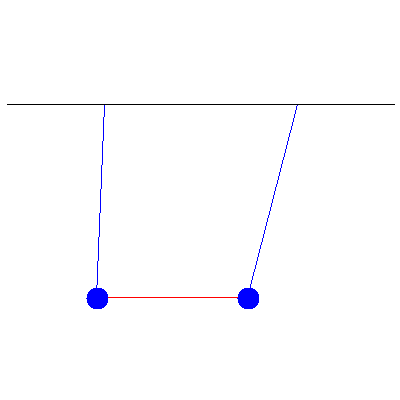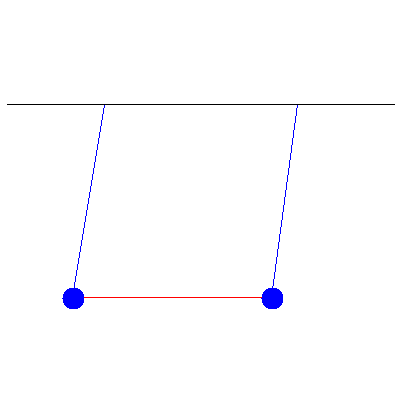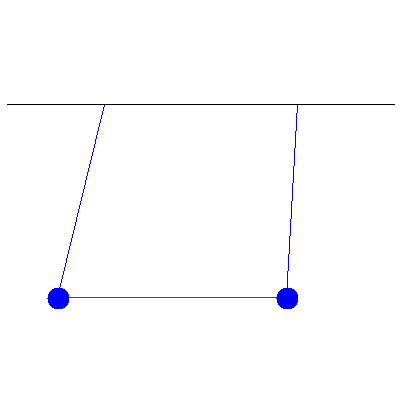If we look at the amplitudes of their displacements, then we see the following: We again see the appearance of beating.













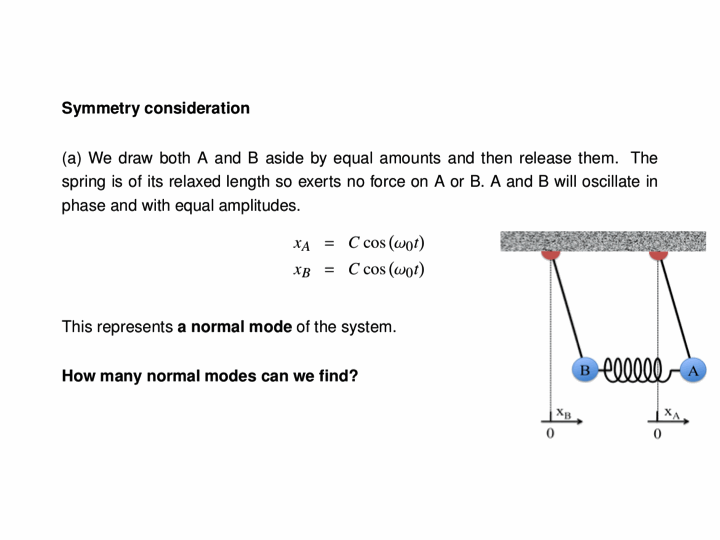
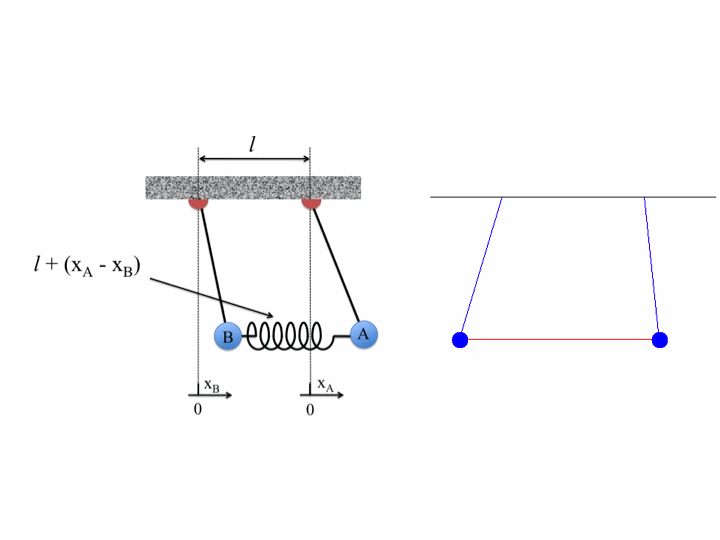
We can use all of this to handle more complicated initial conditions. If the above pendula instead started with initial displacements of 5.2 cm and 1.7 cm, we see 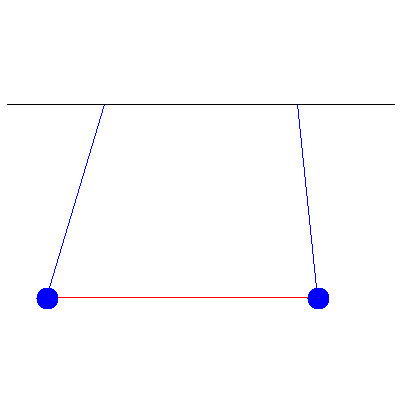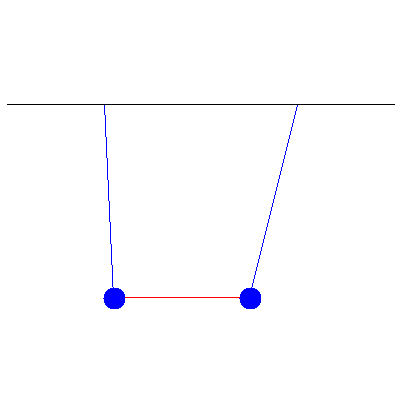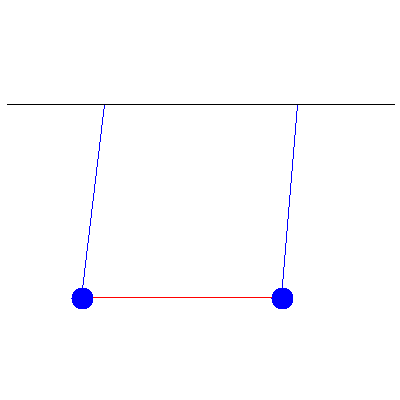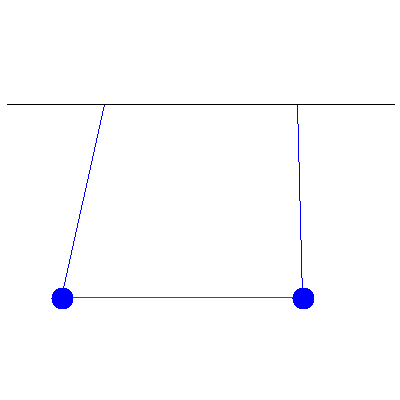This is a combination of the two normal modes shown below:
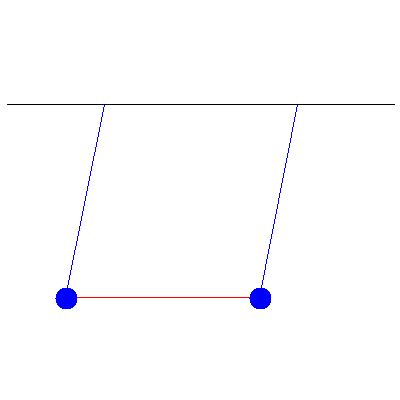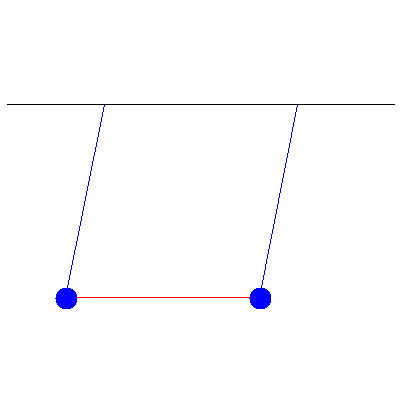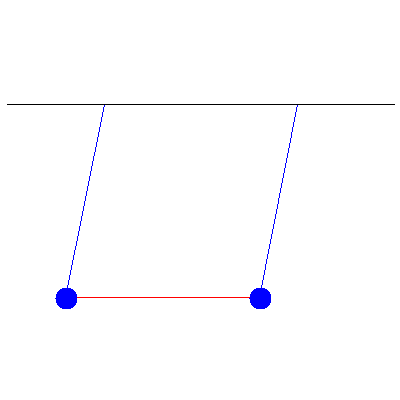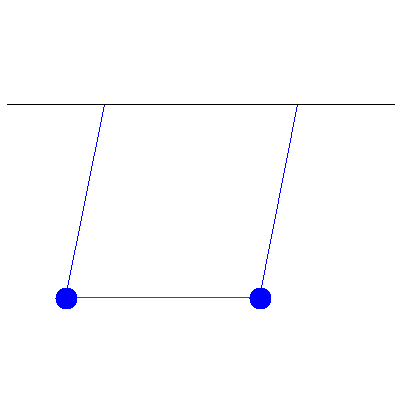
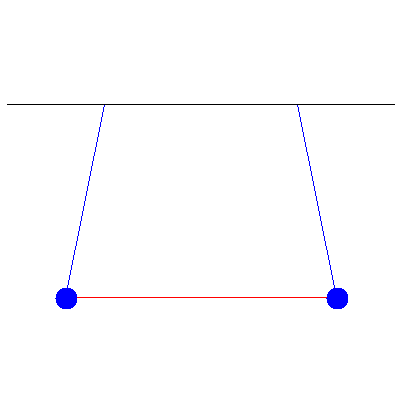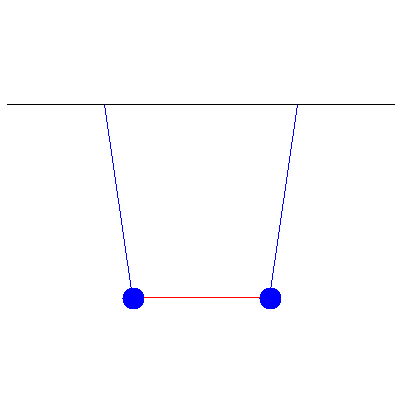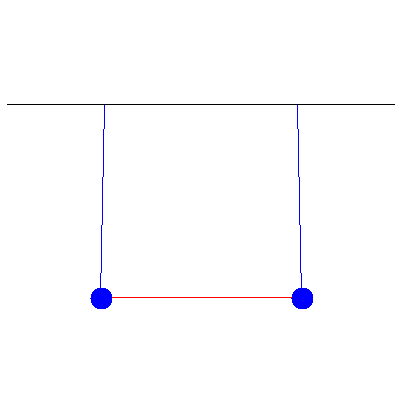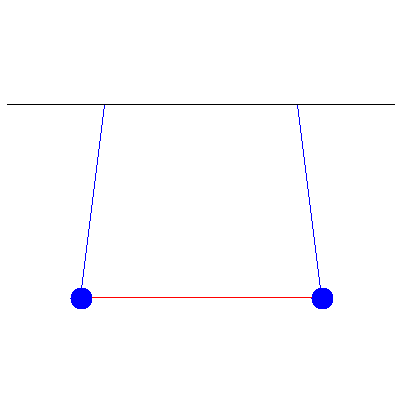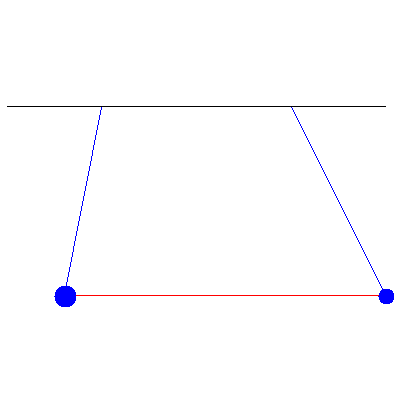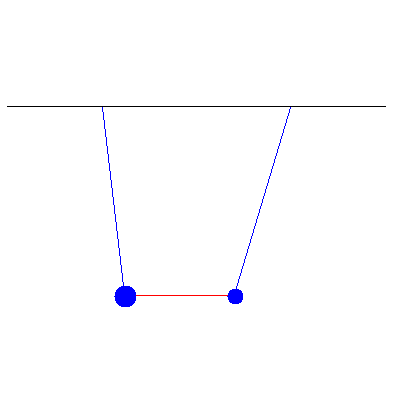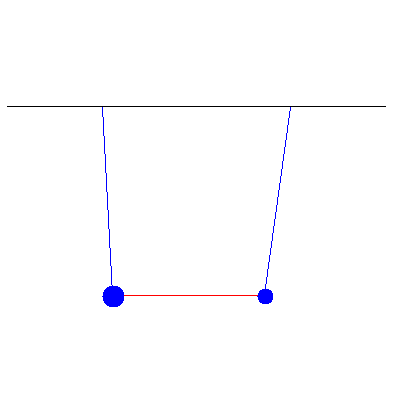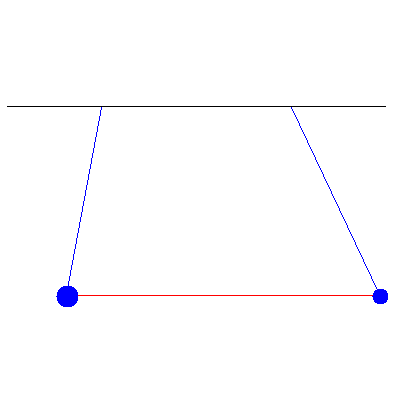
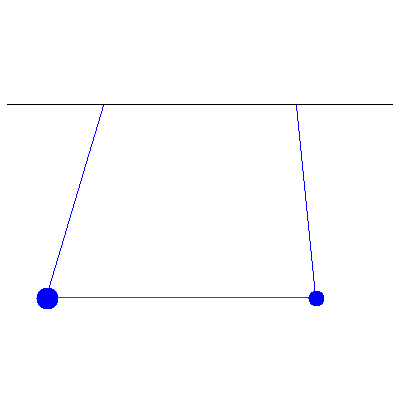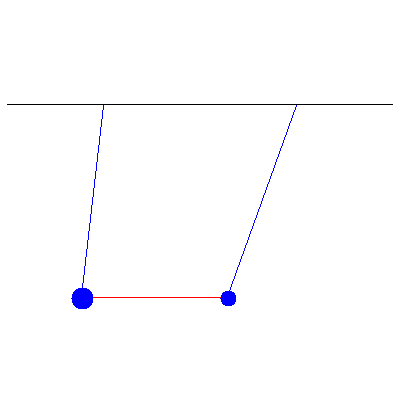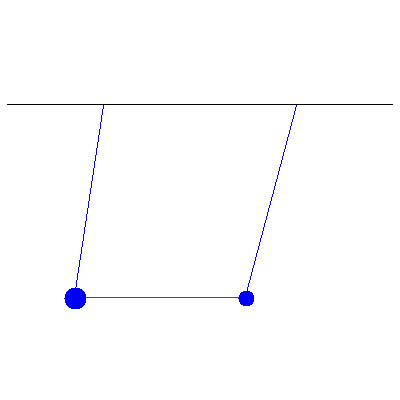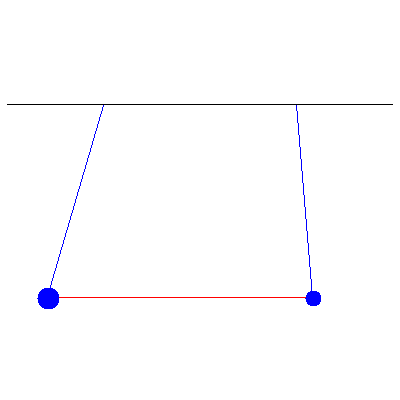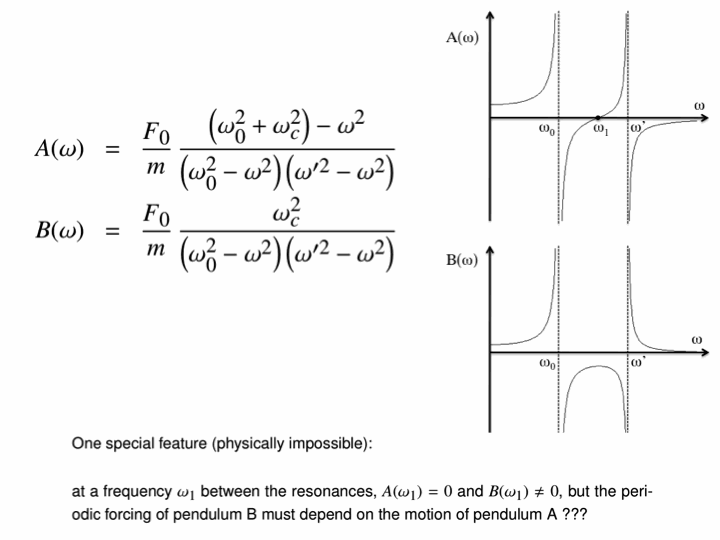
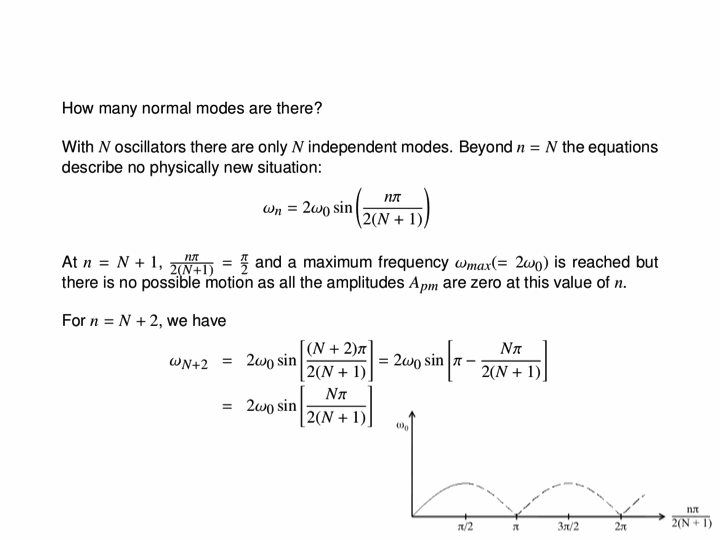
Below is a generic oscillation when the masses are different (and thus no inherent symmetry to the system), one of 100 g and the other of 40 g... ...and the normal modes: To fully solve systems like this one, we must look at a more general approach.