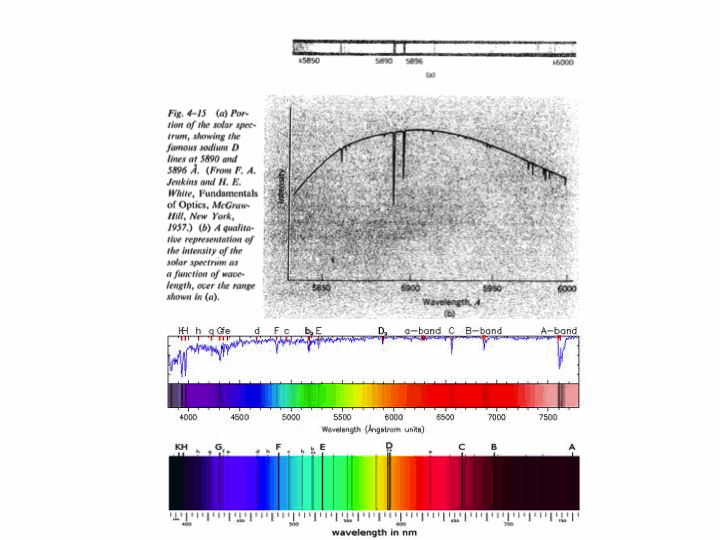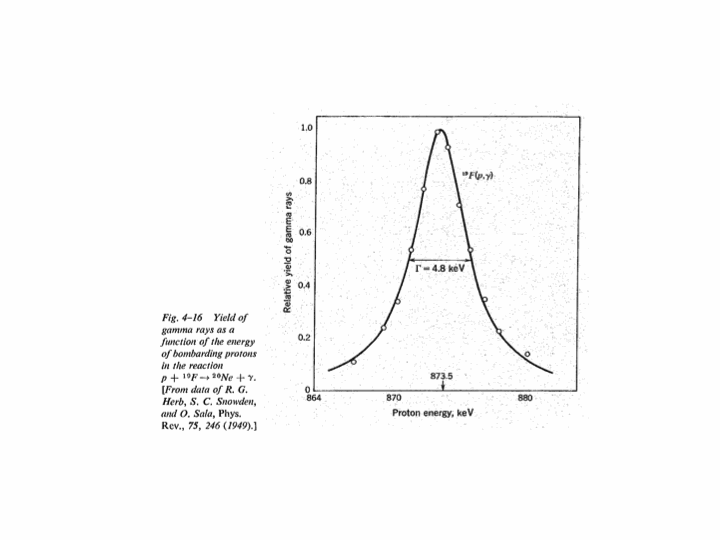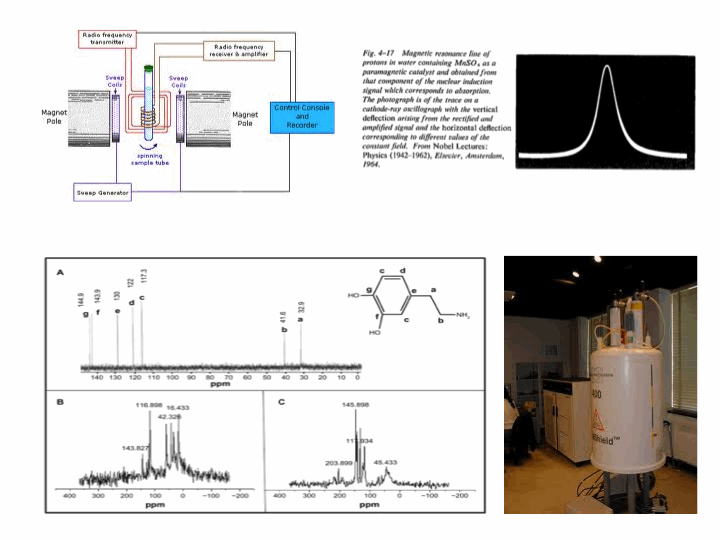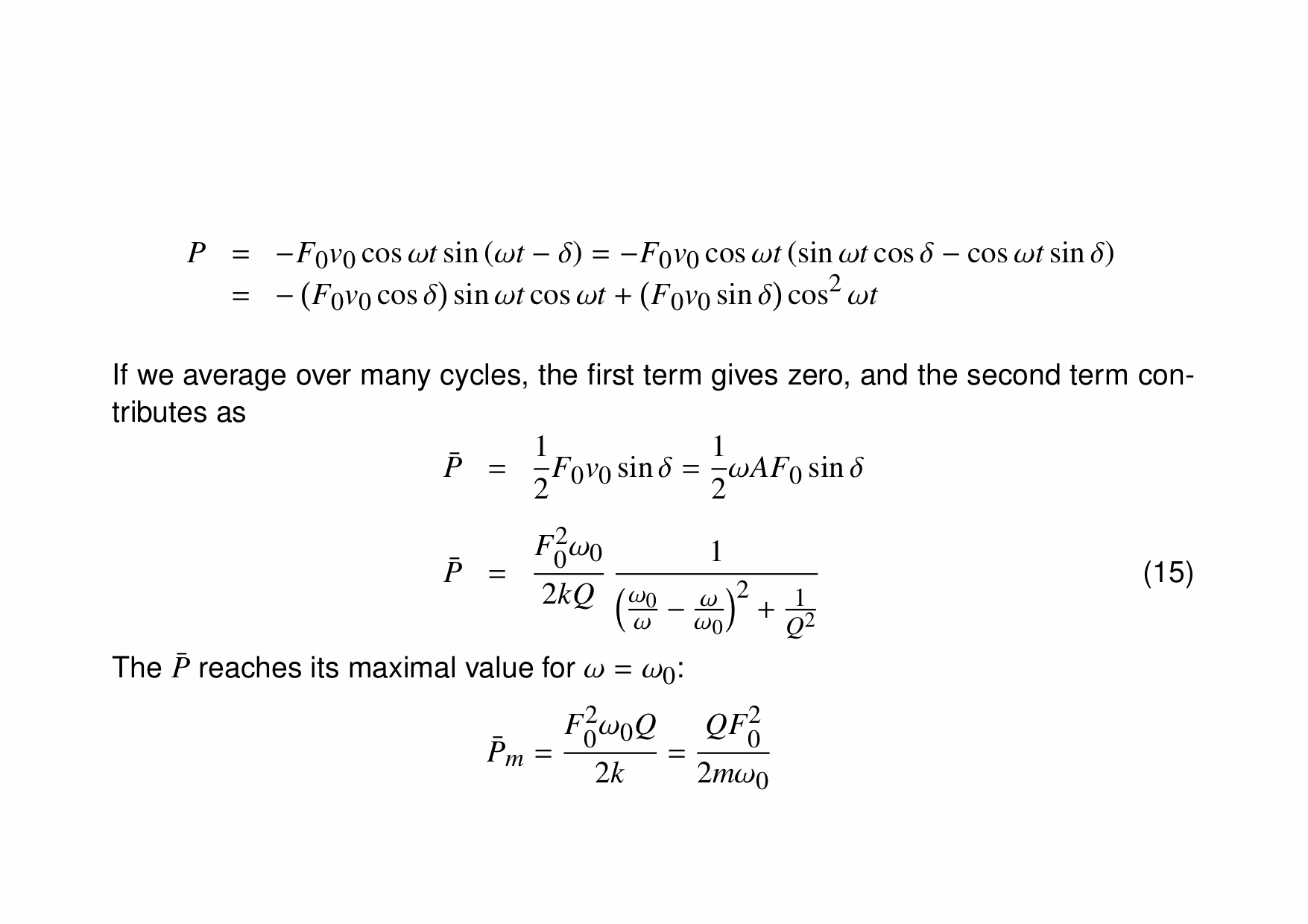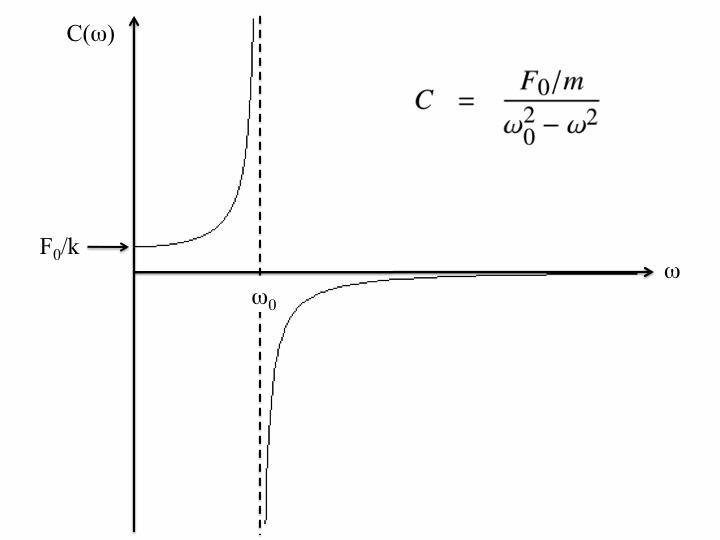
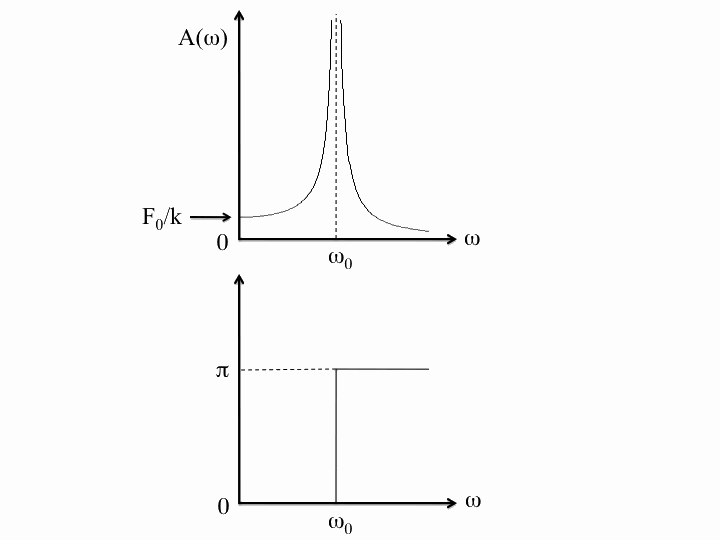
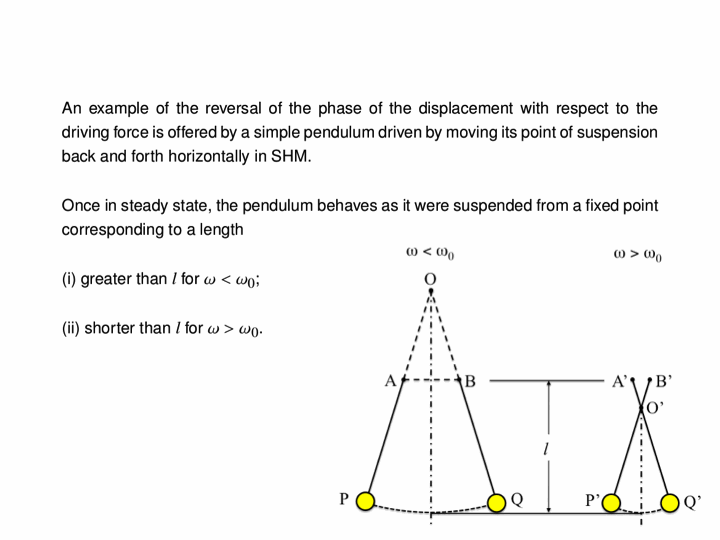
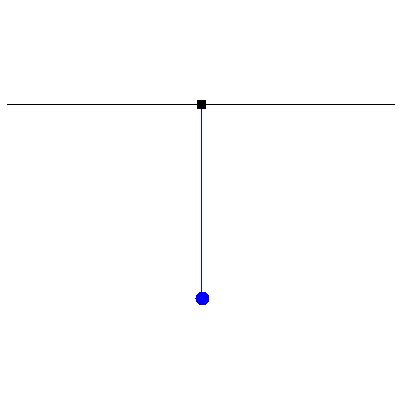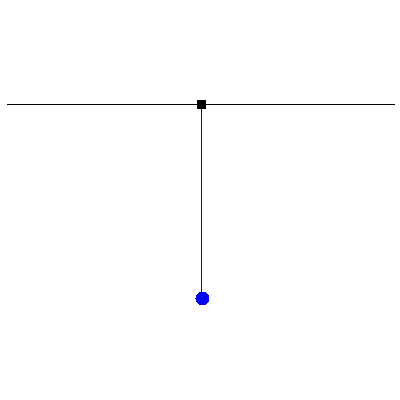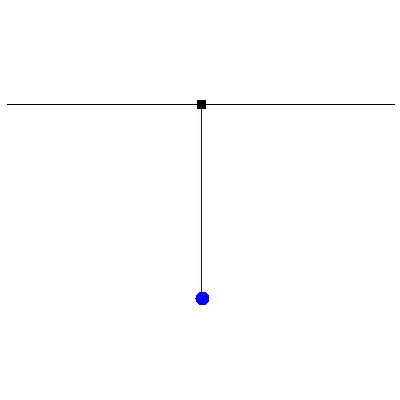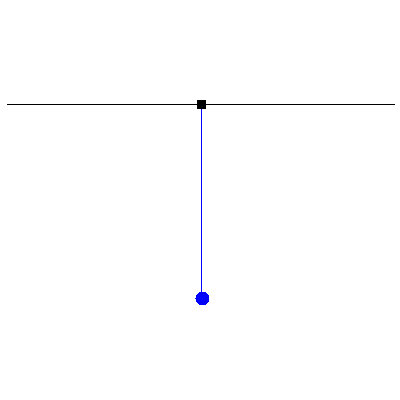
To see the significance of driving an oscillator at resonance, consider the following three animations which depict a (nearly) undamped pendulum of length 38.8 cm (i.e. a natural frequency of $\omega_0=8\pi/5\,\mathrm{rad}\cdot\mathrm{s}^{-1}$). For all three cases, the forcing is done by moving the suspension point back and forth 2 millimetres each way, but with different frequencies. The leftmost has a driving frequency of half the natural frequency, the middle has one of twice the natural frequency and the rightmost is at resonance, namely, the driving and natural frequencies are identical:
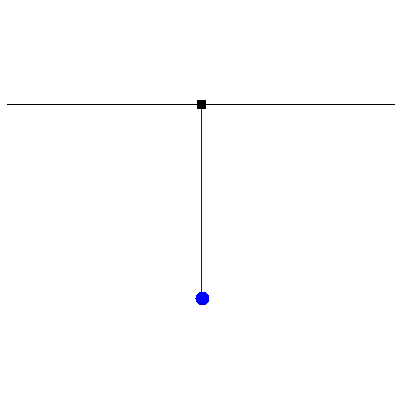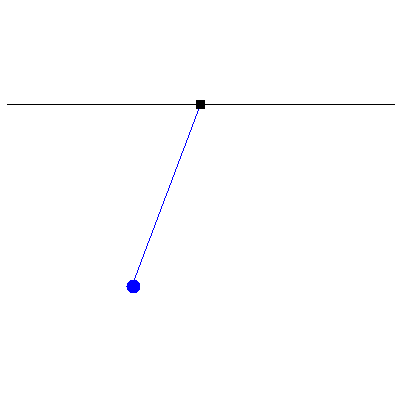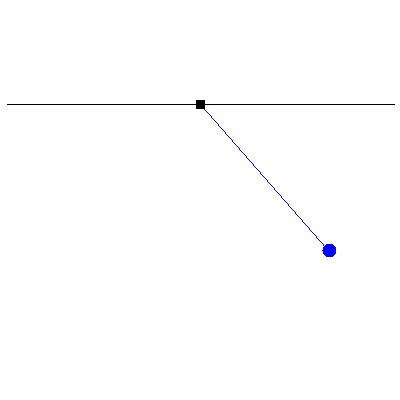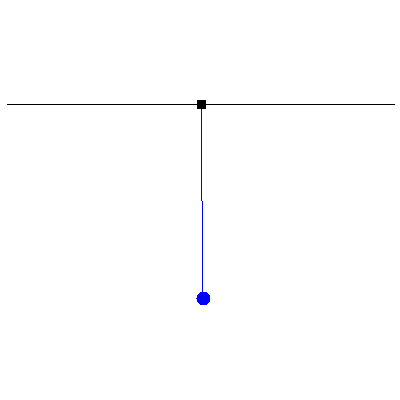
To illustrate this still further, the three animations below show what happens when, instead of driving the suspension point continuously, we give it a "kick", a single oscillation that returns it to its original position. Again, the response at resonance is the most pronounced:










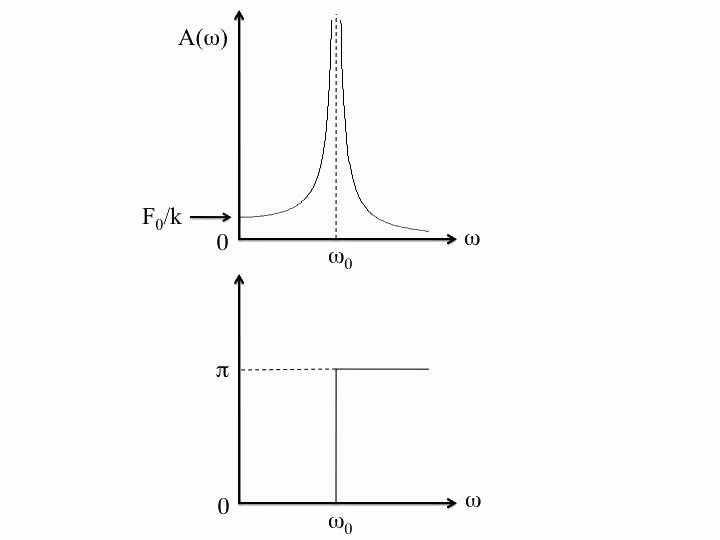
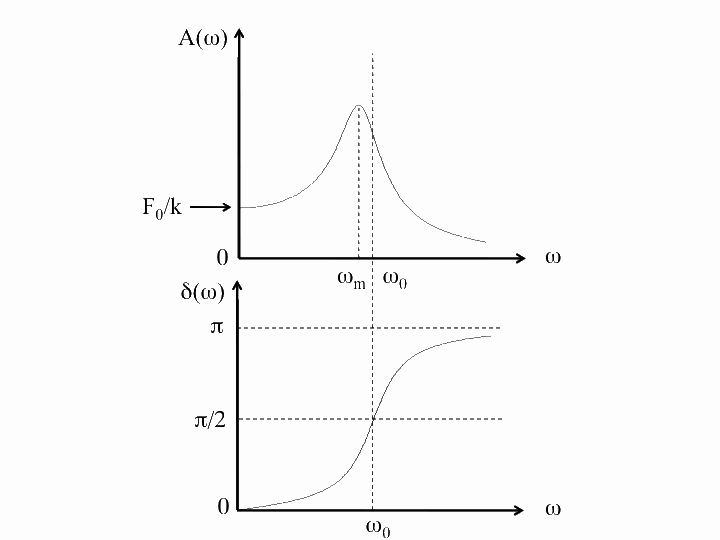
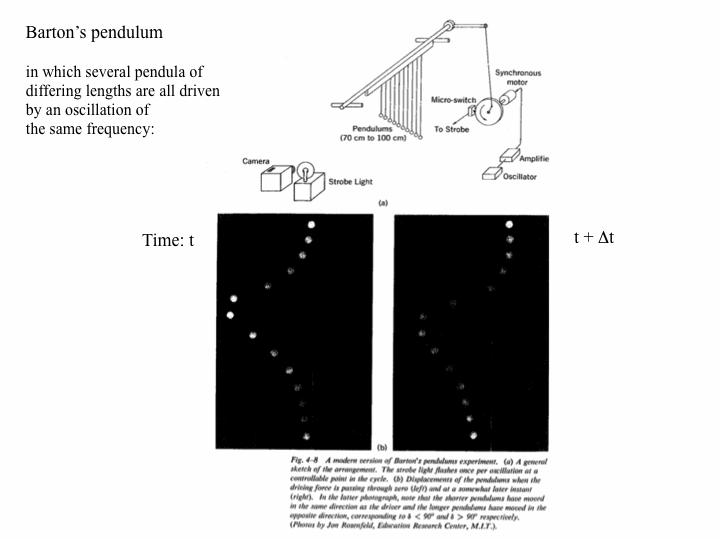
Now that we have included damping, we can take a look at what is known as Barton's pendulum, in which several pendula of differing lengths are all driven by an oscillation of the same frequency. (This is usually done by twisting the rod from which all of them are suspende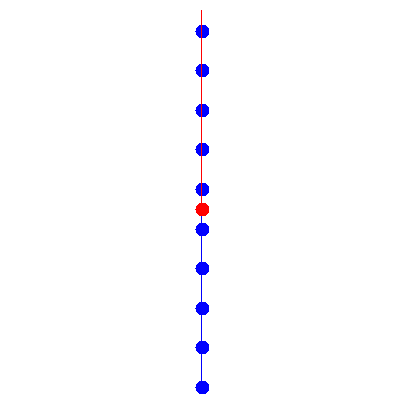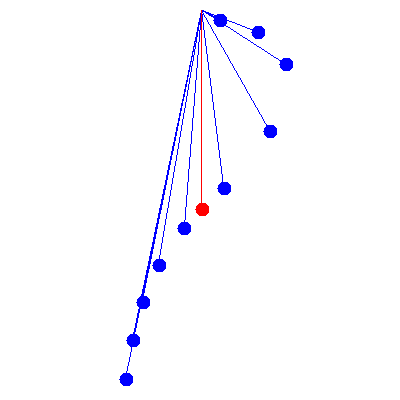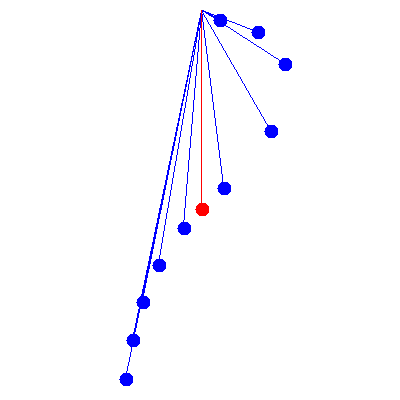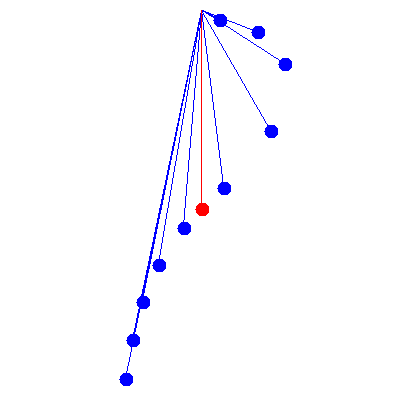d.) In this example, the driving frequency is $\omega=6\pi/5\,\mathrm{rad}\cdot\mathrm{s}^{-1}$ and the damping constant $\gamma$ is the same (i.e. $Q=1$). The ten blue pendula which would have the above behaviour in real life are of lengths from 6.9 cm to 110.3 cm in increments of 13.8 cm. The red pendulum is at resonance, i.e. its natural frequency is identical to the driving frequency, and would be 69.0 cm long. Note that all pendula shorter than this red one lead it, while the longer ones lag behind.




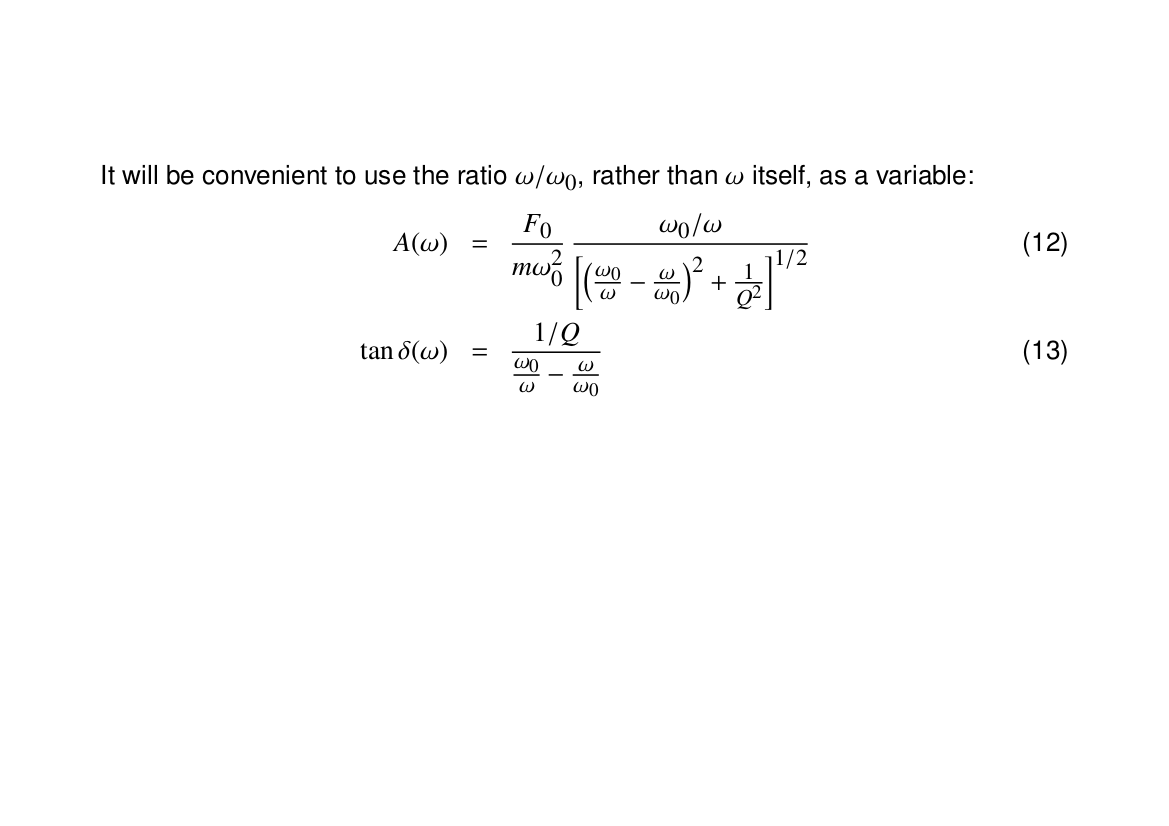
Now we look at how damping affects forced oscillations. Below are three examples using the same pendulum as above, kicked by a half-second long oscillation of amplitude 3.9 cm. The damping constants are, from left to right, half the resonant frequency (underdamped, $Q=2$), 2.5 times the resonant frequency (overdamped, $Q=2/5$) and twice the resonant frequency (critically damped, $Q=1/2$):

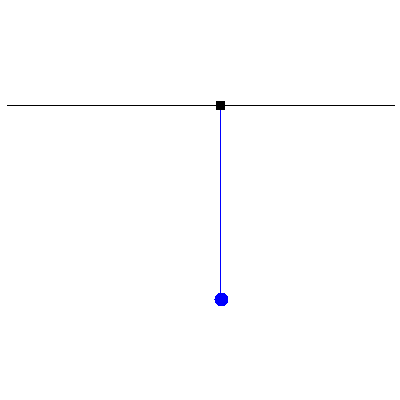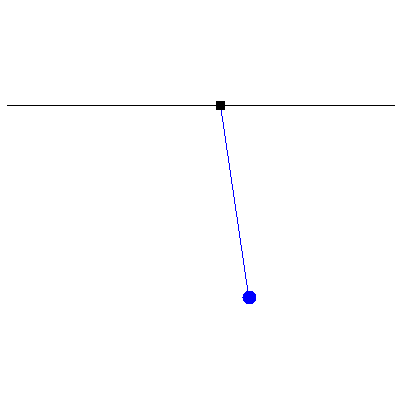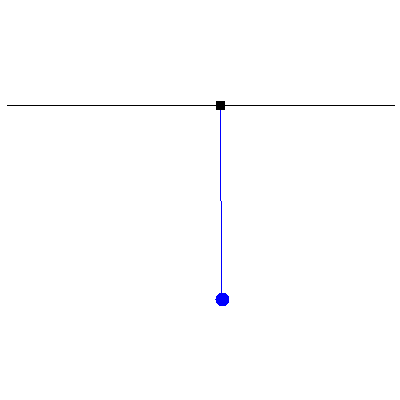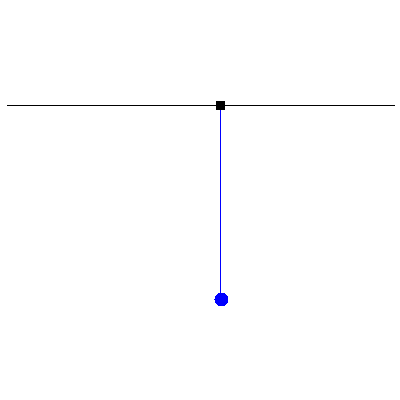
Note that, in both the under- and overdamped cases, the pendulum slighly overshoots its initial position, whereas in the critically damped case, it gradually approaches the vertical without overshooting. This is why the indicator needles in instruments like ammeters and voltmeters are critically damped, so that they quickly approach a final reading rather than wobble about it.