The above five animations illustrate, from top to bottom:

1. A sinewave of the form $A\sin(\omega t)$ with frequency $\omega=8\pi/5\,\mathrm{rad}\cdot\mathrm{s}^{-1}$.
2. A sinewave of the same amplitude as the first, but twice the frequency ($16\pi/5 \,\mathrm{rad}\cdot\mathrm{s}^{-1}$).
3. The same again, except with half the frequency ($4\pi/5 \,\mathrm{rad}\cdot\mathrm{s}^{-1}$).
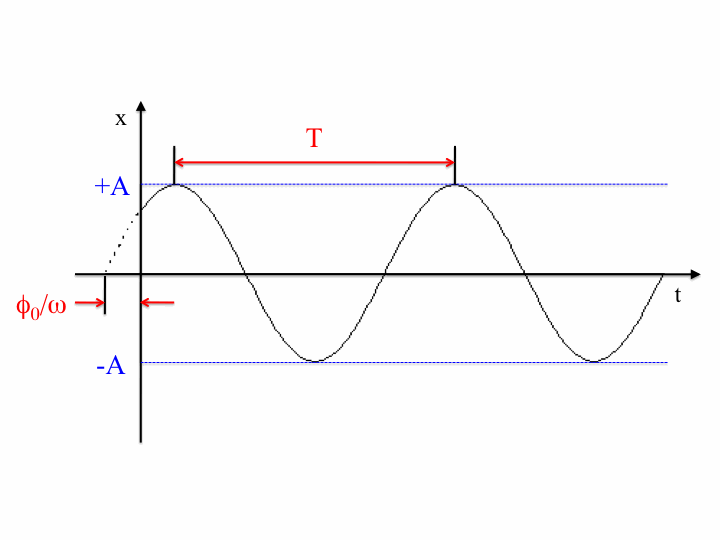
4. A sinewave of the form $A\sin(\omega t+\phi_0)$ with frequency $\omega=8\pi/5 \,\mathrm{rad}\cdot\mathrm{s}^{-1}$ and phase $\phi_0=\pi/4$.
5. A sinewave exactly the same as the first but with amplitude $2A$ instead of $A$.

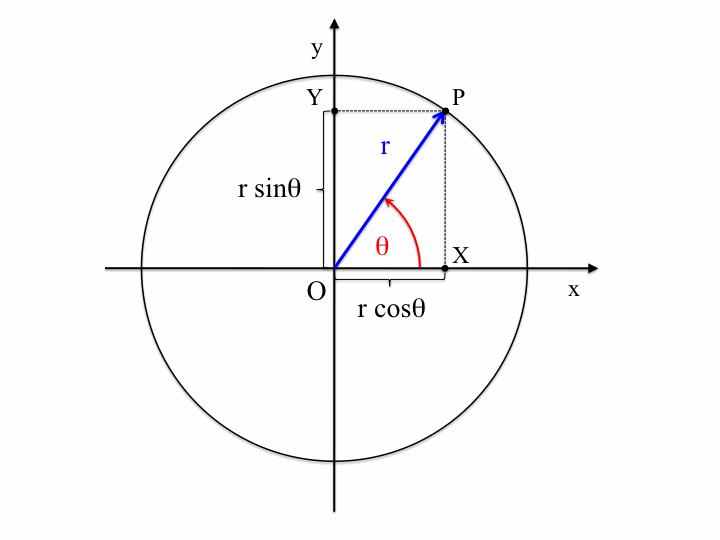
The animation below shows how an oscillatory movement in one dimension (with frequency $16\pi/5\,\mathrm{rad}\cdot\mathrm{s}^{-1}$) can be thought of as a projection of a circular motion in two dimensions: